Dear all,
I’m a beginner in dsge, and I can’t get the log-linearization of the following formula right.
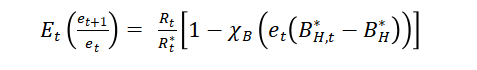
What is the log-linearized form of this formula?
Looking forward to your answer.
Thank you very much.
Dear all,
I’m a beginner in dsge, and I can’t get the log-linearization of the following formula right.
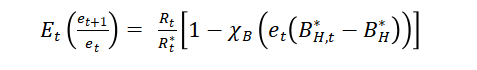
What is the log-linearized form of this formula?
Looking forward to your answer.
Thank you very much.
Dear Eisa Maboudian,
Thank you very much for your answer.
Sorry, I didn’t written clearly before, {B_{H}^{\star}} refers to the steady-state value of {B_{H,t}^{\star}} .
So the last term doesn’t seem to work that way, right?
Looking forward to your answer.
Thank you very much.
Dear all,
After recalculating, I found that the symbol of this formula is wrong, and the correct formula is shown in the figure below.
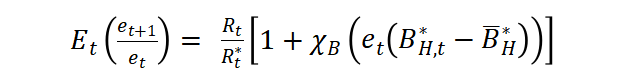
May I ask how to log-linearize this formula?
Looking forward to your answer.
Thank you very much.
I did not see your DSGE model and it’s variables and unfortunately I couldn’t help more than this.
(\hat{e_{t+1}}-\hat{e_{t}})=\frac{\overline{R}}{\overline{R^{\star}}} \star \left[ (\hat{R_{t}} -\hat{R_{t}^{\star}}) + \chi_{B}\star \overline{e} \star \overline{B_{H}^{\star}}(\hat{R_{t}} -\hat{R_{t}^{\star}} +\hat{e_{t}}+ \hat{B_{H,t}^{\star}}) - \chi_{B} \star \overline{e} \star \overline{B_{H}^{\star}} \star (\hat{e_{t}} + \hat{R_{t}} - \hat{R_{t}^{\star}}) \right]