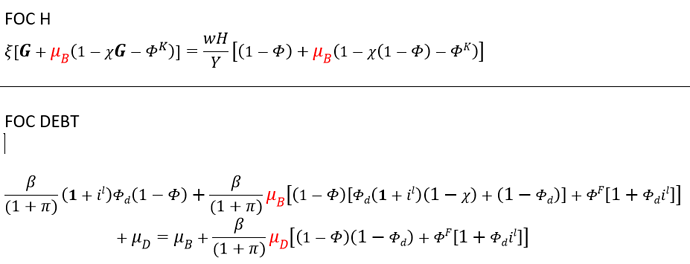Hi
I have a profit function for the firm and I define a constraint for the firm. And I solve this with a Lagrange multiplier. My question is what is the logical value for the Lagrange multiplier in the Steady State. Less than one or more than one? positive or negative? Or there is no specific law .or it depends on our equations and our problem. For example, (1.10 ) was obtained for me
If the constraint is binding, the multiplier must be positive (if set up with the usual sign convention).
The problem I have with this is:
My optimization is as follows:
After obtaining the first-order conditions and obtaining the Steady State equations: I have the following equations in Steady State:
And two other equations
Now when I calibrate the parameter data, the Lagrange coefficients in the steady state are negative.Of course, if I change the parameters a little, they can be positive. For example, with a phi_ss of 0.15, the Lagrange coefficient is negative, but when I take a phi of 0.30, the Lagrange coefficient becomes positve.
My question is that a negative Lagrangian coefficient(in the steady state) indicates that our equations or calibration are wrong, and we need to be more careful in both.?.