I’m running a model using Jaimovich-Rebelo preferences (2009): u(c_t,n_t)=\left(c_t-\psi X_t\frac{n_t^{1+\xi}}{1+\xi}\right)^{1-\sigma}, where X_t=c_t^{\gamma}X_{t-1}^{1-\gamma}, and as mentioned in the article \gamma=0 makes u correspond to GHH preferences, and \gamma=1 to KPR preferences.
My model has Calvo stickiness and transaction costs, including this type of preferences I get as response to TPF shock when I set \gamma=0 (c_t= consumption, n_t=labor, w_t=wages, a_t=TPF):

And when I set \gamma=1:
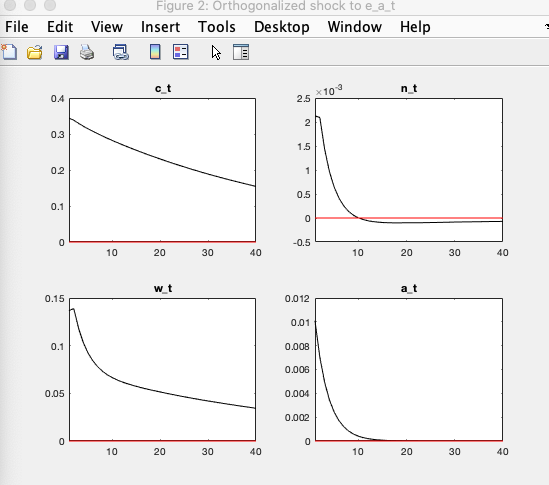
I expected labor to decline in GHH case (\gamma=0) but it doesn’t. Is that behavior right and I’m misinterpreting something about the differences between KPR-GHH-additively separable preferences?
Thanks!!