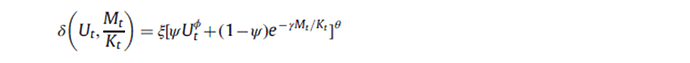Is it feasible to estimate variable depreciation rates using DSGE models, and which estimation variable should I choose (filtered variable, smoothed variable, updated variable, or forecast variable)

Estimation ML/Bayesian estimation
1

Dear Prof jpfeifer;

Hello, I have a question to ask you. I tried to design a small DSGE model to estimate China’s variable capital depreciation rate over the years. I have uploaded the code and data, and the preliminary results have been completed by dynare. But I now have a question whether I can use this method to estimate the variable depreciation rate over the years (for macroeconomic capital stock accounting purposes), Which variable in the simulated economy (filtered variable, smoothed variable, updated variable, or forecast variable) can be used as the value of the estimated variable depreciation rate? I look forward to your help in answering my questions. Thank you very much.
MODLE.MOD (3.7 KB)
dataln.mat (2.1 KB)

2

Usually, you would use the smoothed variables. They are your best estimate as of the end of the sample of what has happened during the sample period.

3

Dear Professor jpfeifer,

Hello! Thank you very much for taking time out of your busy schedule to answer my questions. As a beginner, I also met some other questions, I hope you can help me answer them again, I have uploaded the relevant documents.
MODLEC.MOD (3.7 KB)
dataln.mat (2.1 KB)

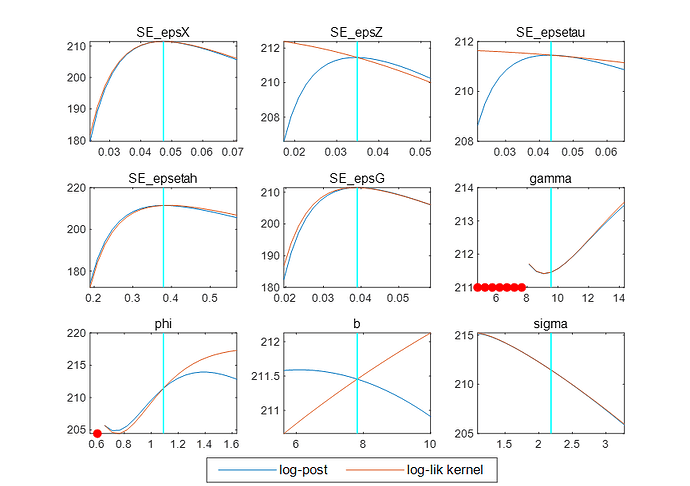
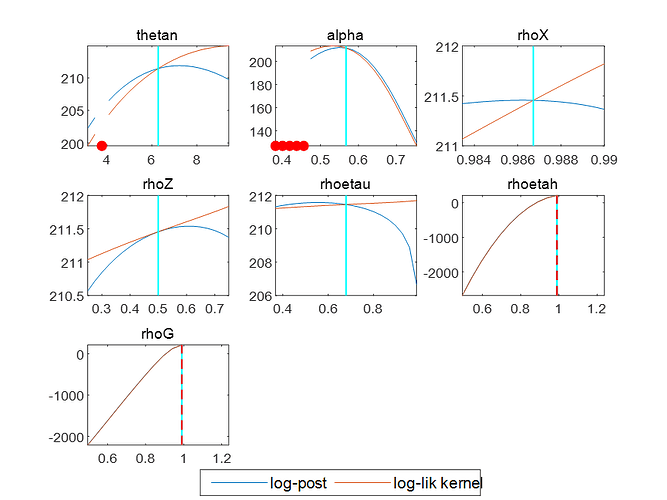
(1) The mode check plots of the model parameters are not satisfactory, I would like to ask what is the reason for this, is it the wrong choice of the prior distribution values of the parameters? Can I try to adjust the prior values of the parameters? Or is there something else wrong with my model?

image
image865×610 50.2 KB

image
image865×648 39.3 KB

(2) In my model code, D is variable depreciation rate variable, and depreciation rate is a function of capital utilization rate (U), capital stock (K) and capital maintenance cost (M). The formula designed is as follows:

image
image865×80 12.4 KB

When you said in your reply that smooth variables were used, did I directly use the mean of smooth variables of D in the estimated result (oo_) as the final depreciation rate over the years? Or do you need to bring the smoothed variable mean of U and M in the estimated result (oo_) into the above equation, and use the posterior estimates of the parameters to calculate the final depreciation rate over the years through the above equation? Because I tried to get the difference between the depreciation rates of the two methods (the observed variables I used were China’s annual GDP, total consumption and employment from 1978 to 2020, which were obtained by using HP filtering after taking the logarithm).
Sorry to bother Professor jpfeifer again. Looking forward to your reply. Best wishes!

4
  1. You don’t handle parameter dependence correctly.
  2. Your data is not correctly matched to the model. For example Y in the model is the output level with steady state 1.43427, but in the data is it mean 0.
  3. Typically, you would use the mean smoothed variables over the posterior.
5

Hello Professor, thank you again for your reply. I’m sorry that I can’t quite understand it. What do you mean by parameter dependence? Could you give me a detailed example? As for your second point, the average value of the Y is 0, does it mean that the parameter assignment on my side is as close to 0 as possible? For example, Y is calculated by the steady-state value of the endogenous variable and the parameter assignment in the steady-state state, does it mean that the steady-state value of the relevant endogenous variable and the parameter assignment should make the steady-state value of Y as close to 0 as possible? Thank you very much Professor JPFEIFER, looking forward to your reply!

6

Please have a look at Pfeifer (2013): “A Guide to Specifying Observation Equations for the Estimation of DSGE Models"

7

Thank you very much Professor JPFEIFER,