I calibrated the size of a government expenditure shock to fit certain data moment. After the calibration, I want to do some IRFs analysis, but if I use the size I found in the calibration I get implausible (or hard to interpret) results, particularly with an expansionary govt. expenditure shock, I get that output falls as a response to the shock.
But when I reduce the size of the shock for the irfs analysis, to a smaller value the shock behaves more as expected. Is it wrong that I change the size of the calibrated shock in order to interpret the results better? Thanks for your advice.
At first order, what you describe cannot happen due to linearity. At higher order, you can select different shock sizes for your IRFs, but need to justify the selected value. Why should it be more representative than a 1 standard deviation shock? Also note that standard deviation of the shocks and the shock size in an IRF are two different objects. It would be wrong to change the overall standard deviation.
1 Like
The justification for the calibrated value (which among other things is rather high I think, around 0.2), is that it allows for an important correlation observed in data to hold in the theoretical moments of the model, I did a visual identification and this is the only parameter that has the ability to move that correlation to the desired values.
In the other hand, when making an IRFs analysis if I use that same shock size, happens what I described before (indeed I’m solving the model at 2nd order). The only justification for changing the size of the shock (when analyzing irfs only) would be better display of the magnitude of the impact in other variables, e.g. set the size at 1% or a similar “standard” value, and being able to show that if that shock is of that size, then consumption deviates 2.5% (for example). Is that enough of a reason, or that would be wrong?
Also, the way I’m calibrating the size of shocks is with a coefficient, i.e., sh_t = 0.9*sh_t(-1) + size_shock*epsilon_t, thus epsilon_t has stderr=1 and the parameter size_shock controls for the magnitude of deviations of the exogenous, and is the calibrated parameter.
Thanks!!
As I said, you should not change the standard deviations, but only the shock size for the IRFs. You need to do this manually using simult_.
1 Like
But why do I need to use simult_? What would be the difference between doing it that way and just adjusting the size through the parameter size_shock? Also, how should be done with simult_? Thanks a lot.
Because manipulating size_shock will change the ergodic distribution of the model. You want to keep that constant and only do an IRF to a smaller shock.
2 Likes
I did not know that, thank you! I was checking the documentation included in the simult_.m file of Dynare, and I wonder what should I introduce in the ex_ arguments for the mentioned purposes?
Also, as I notice that this function will return a matrix containing simulated time series for endogenous variables, this means I should estimate a VAR on those series and then calculate IRFs on that VAR manually, of is there a more direct way to get the IRFs from these simulations, may you have an example? Thank you!
Thank you. I just was able to put it to work (I think), and I have two questions:
-
If I’m going to analyze more than one shock with IRFs, I need to perform the simult_() routine for each one at a time and letting the rest as zero in the shock_matrix, right?
-
When performing a TFP shock such that the increase in the variable when the shock happens is 10 basis points, output goes rises far more than 10 basis points, and even output seems not returning to the ss but a different ss. See the image below:
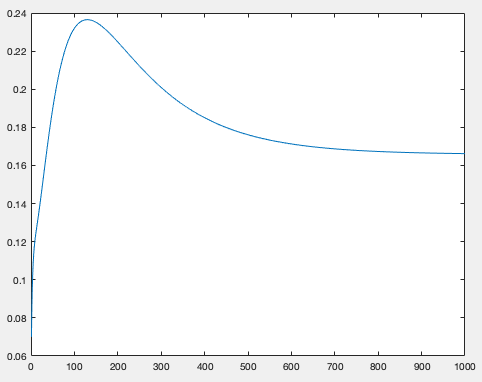
What am I doing wrong? (Worth mentioning, that my model doesn’t feature any unit root or something similar, every variable is and is meant to be stationary.)
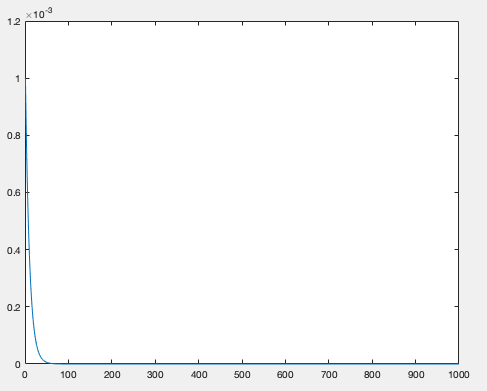
Also, this is how the TFP shock looks like (which behaves as expected).
You need to ask yourself which type of IRF you want to generate. At higher order that is not trivial. You can see this from the fact that your current IRF converges to the stochastic steady state, which is different from the deterministic one. Search the forum and have a look at RBC_state_dependent_GIRF.mod - Google Drive (which
I still need to update and port to Github.)
1 Like
Hi. I think I understand more now, and came to the conclusion that what I want is the “regular” Cholesky-decomposed irfs (default with stoch_simul). And now I’m in the need of calculating only inflation-increasing shocks irfs, but naturally not all my shocks produce a positive inflation response. Thus I need to only flip the sign, of some shocks such that all of them produce the desired sign for inflation response. If I only flip the sign, without altering the absolute value of size_shock, am I perturbing the ergodic distribution of the model, or is it right? Thank you.
Flipping the sign does not alter anything as the variance is unaffected.
1 Like

