I want to estimate model using IRF Matching. Model is working but parameters are not estimated. What to do? code and files attachedbuild_companionform.m (608 Bytes) IRF_matching_objective.m (1.1 KB) get_empirical_IRFs.m (5.7 KB) IRFNEW.mod (4.4 KB) finaldata.xlsx (20.7 KB)
What do you mean with
?
Note that your plot commands should be
plot(1:options_.irf,oo_.irfs.y_eetar);
Dear Professor,
Sorry I had lost the password of this ID that why text you from my old account.
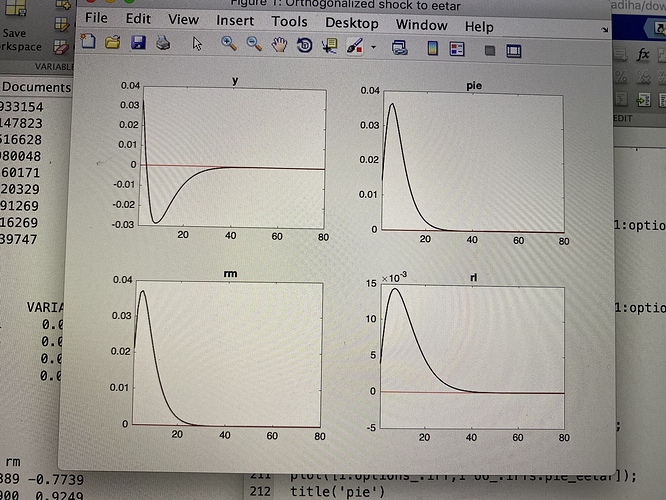
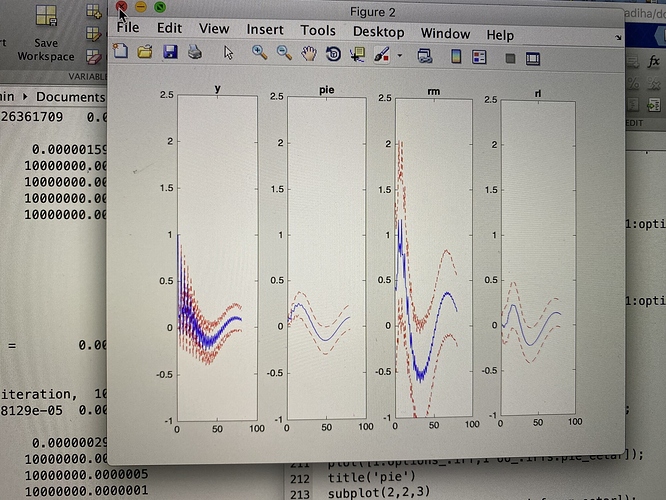
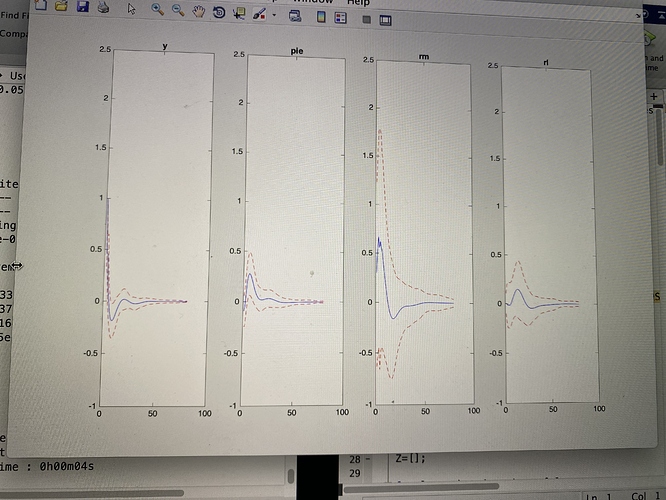
Figure 1 is the calibration results. what are the results of figure 2 & 3. As, I think that figure 2 is IRF-matching results and figure 3 contains IRFs of empirical shock responses? plz comment.
one more thing, You have used code scheme in Your IRFs matching example:
figure
subplot(2,1,1)
plot(1:options_.irf,IRF_empirical(:,1),1:options_.irf,IRF_model(:,1),1:options_.irf,IRF_quantiles(1,:,1),‘r–’,1:options_.irf,IRF_quantiles(1,:,2),‘r–’);
title(‘G’)
subplot(2,1,2)
plot(1:options_.irf,IRF_empirical(:,2),1:options_.irf,IRF_model(:,2),1:options_.irf,IRF_quantiles(2,:,1),‘r–’,1:options_.irf,IRF_quantiles(2,:,2),‘r–’);
title(‘Y’)
legend(‘Empirical’,‘Model’)
Is this can apply in my model for four variables?
The values given in x-opt-hat are optimized or estimated?
Figure 2 is the empirical IRFs, which are oscillating. That is not a good sign. Figure 3 should compare empirical and model IRFs after estimation. But you screwed up the code, as outline by me previously.
The x_opt are the estimated parameters.
Thnx professor for your reply.
How can I improve figure 2. I should transform data based on your "observation equation article’??
I had used the code suggested by you and I got this result.
Then I modified your code, which you have indicate in your example. I use this code:
figure
subplot(2,2,1)
plot(1:options_.irf,IRF_empirical(:,1),1:options_.irf,IRF_model(:,1),1:options_.irf,IRF_quantiles(1,:,1),‘r–’,1:options_.irf,IRF_quantiles(1,:,2),‘r–’);
title(‘y’)
subplot(2,2,2)
plot(1:options_.irf,IRF_empirical(:,2),1:options_.irf,IRF_model(:,2),1:options_.irf,IRF_quantiles(2,:,1),‘r–’,1:options_.irf,IRF_quantiles(2,:,2),‘r–’);
title(‘pie’)
subplot(2,2,3)
plot(1:options_.irf,IRF_empirical(:,3),1:options_.irf,IRF_model(:,3),1:options_.irf,IRF_quantiles(3,:,1),‘r–’,1:options_.irf,IRF_quantiles(3,:,2),‘r–’);
title(‘rm’)
subplot(2,2,4)
plot(1:options_.irf,IRF_empirical(:,4),1:options_.irf,IRF_model(:,4),1:options_.irf,IRF_quantiles(4,:,1),‘r–’,1:options_.irf,IRF_quantiles(4,:,2),‘r–’);
title(‘rl’)
legend(‘Empirical Model’)
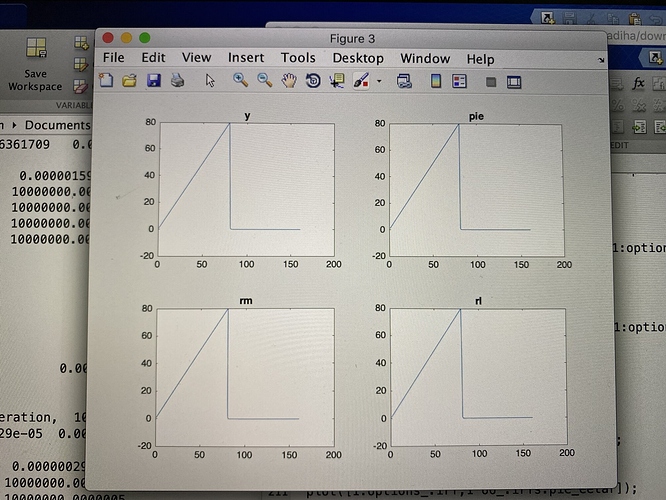
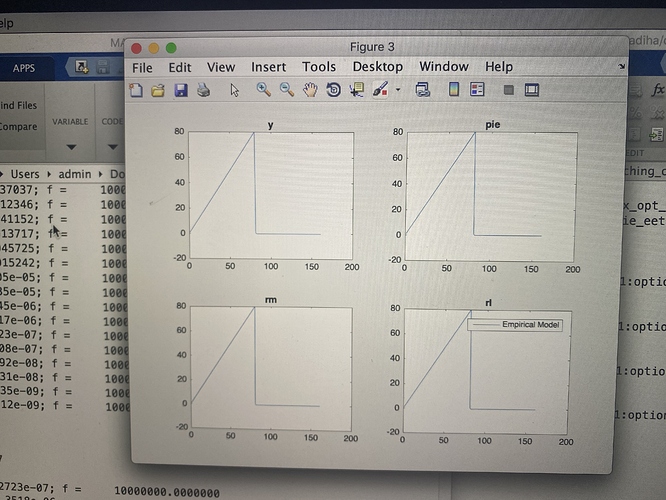
I am also thinking that figure 3 is not comparing empirical & model IRFs and I don’t know the reasons, although I adopt your code fully.
Sorry for long post. if x-opt are estimated parameters, then where are their standard errors in workspace?
You need to be a lot more careful. You are using starting values for the optimization that are not in the bounds that you defined. Also, it should be
%select IRFs for matching
IRF_mat=[IRFs_point(y_pos,:)' IRFs_point(pie_pos,:)' IRFs_point(rm_pos,:)' IRFs_point(rl_pos,:)'];
instead of the strings that you currently defined.
Dear Professor,
I worked again on code & objective function. Now, getting this error.
Error using *
Inner matrix dimensions must agree.
Error in get_empirical_IRFs (line 51)
bhat = kron((Z*‘Z’)\Z,eye(nvars))*y(:);
Error in IRFNEW (line 289)
[IRF_empirical,IRF_weighting,IRF_quantiles]=get_empirical_IRFs(80)
Error in dynare (line 235)
evalin(‘base’,fname) ;
Is this problem is related to use more parameters than variables to be estimated?get_empirical_IRFs.m (5.8 KB) IRF_matching_objective.m (1.3 KB) IRFNEW.mod
(5.8 KB)
codes are attached: plz help
You created a total mess in your files. Instead of appropriate transpose signs, you put in a bunch of quoted strings.
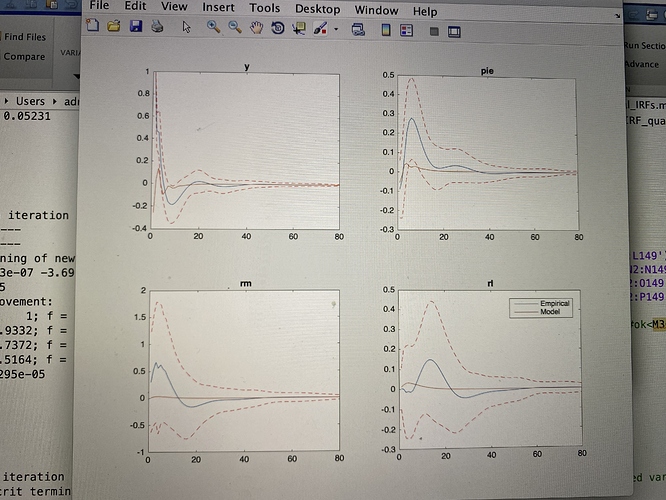
Sorry Professor, I take my code elsewhere. Now, these are my final results after modification of my data using your article.
plz comment
That looks ok. Your model - as expected - has a hard time getting the delayed response right.
Thnx professor, one more thing?? How can I improve my estimated parameters values??? These are in negative, these values should be positive.
Then you need to impose proper bounds during the estimation.
thanks for your reply Professor. I want to ask that estimated parameters are accompanied by their standard errors also. where are standard errors in workspace?? or there is any other way to report estimated parameters?
I did not implement the required sandwich estimator to get the standard errors of the parameters. You would need to do that yourself.
can you please guide me how to get standard errors?
Dear professor, kindly suggest how to calculate standard errors for estimated parameters??
Dear Professor, hope you are doing well.
Problem is my estimated parameters are in negative although I set lower and upper bounds positive and use calibration values as a starting point. I am changing my lower and upper bounds but still found negative estimates. Plz help. code attachedIRFNEW.mod (5.9 KB) IRF_matching_objective.m (1.1 KB)
You need to think yourself before posting here. You use
if any (xopt<=0.4) || any (xopt(1)>=1);%make sure roots are between 0 and 1
fval=10e6+sum([xopt].^2); % penalty function
return
end
That filters out any value smaller than 0.4. But then you start estimation with
x_start=[0.5 0.4 0.36 0.5 0.75 0.5]'; %use calibration as starting point
which has two values not satisfying your own bound.