Hello!
I have constructed a simple NK model that includes a household sector, an intermediate goods sector, an aggregated goods sector, the government, and the central bank. Households interact with the production sector by supplying labor to intermediate firms. Their interaction with the government occurs through the purchase of bonds, from which they earn interest income. The central bank sets the interest rate.
Intermediate goods producers interact with households by paying wages and distributing profits. The aggregation sector combines various intermediate goods into a single final good, which is then allocated for household and government consumption as well as investment. Additionally, firms own capital.
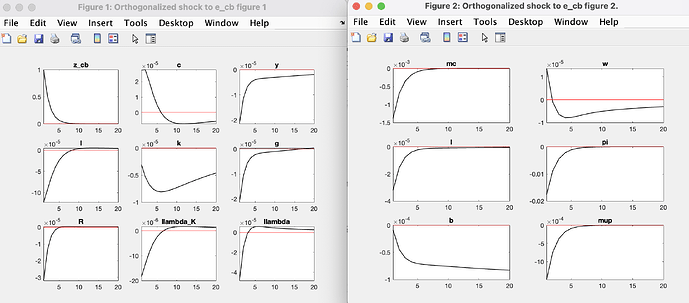
I am trying to introduce a borrowing constraint for the production sector (intraperiod loan) into the model, following the approach of Sims (2017) (https://sites.nd.edu/esims/files/2023/05/financial_constraint_2017.pdf). However, when I incorporate this constraint and analyze a positive monetary shock, I observe an unexpected outcome: instead of rising sharply, the interest rate drops significantly in response to the shock, even though the shock is applied directly to the central bank’s policy rate. Without the constraint, the interest rate responds to a positive monetary shock by increasing.
The monetary policy shock is specified as:
z_cb = rhocb * z_cb(-1) + e_cb;
And the central bank’s interest rate rule is:
R/STEADY_STATE(R) = (R(-1)/STEADY_STATE(R))^rhocb * (((pi / STEADY_STATE(pi))^(gamma_cb))^(1 - rhocb)) + z_cb;
Could you help me understand why this is happening?