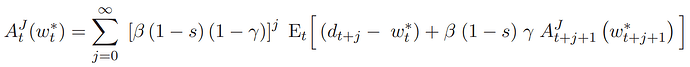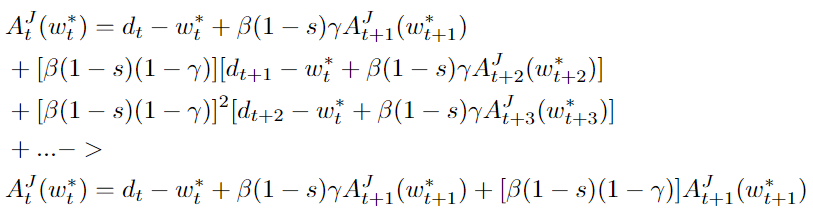pb11
1
Hello,
I am trying to rewrite the following equation recursively, but I am not sure if I am doing everything right:
The first result I arrived at is the following (leaving out the expectation operator):
I am not entirely sure that this result is correct: What concerns me most is the variable w_t^*
I would really apreciate your help. Thank you
ps. This is equation of (2) from this work
I am getting
\begin{align}
A_t^J\left( {w_t^*} \right) =& \sum\limits_{j = 0}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}{E_t}\left[ {\left( {{d_{t + j}} - w_t^*} \right) + \beta \left( {1 - s} \right)A_{t + j + 1}^J\left( {w_{t + j + 1}^*} \right)} \right]} \hfill \\
=& \left( {{d_t} - w_t^*} \right) + \beta \left( {1 - s} \right)E_tA_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
&+ \sum\limits_{j = 1}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}{E_t}\left[ {\left( {{d_{t + j}} - w_t^*} \right) + \beta \left( {1 - s} \right)A_{t + j + 1}^J\left( {w_{t + j + 1}^*} \right)} \right]} \hfill \\
=& \left( {{d_t} - w_t^*} \right) + \beta \left( {1 - s} \right)E_tA_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
&+ \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]\sum\limits_{j = 0}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}{E_t}\left[ {\left( {{d_{t + 1 + j}} - w_t^*} \right) + \beta \left( {1 - s} \right)A_{t + 1 + j + 1}^J\left( {w_{t + 1 + j + 1}^*} \right)} \right]} \hfill \\
=& \left( {{d_t} - w_t^*} \right) + \beta \left( {1 - s} \right)E_tA_{t + 1}^J\left( {w_{t + 1}^*} \right) + \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]\sum\limits_{j = 0}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}{E_t}\left[ {\left( {w_{t + 1}^* - w_t^*} \right)} \right]} \hfill \\
&+ \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]\sum\limits_{j = 0}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}{E_t}\left[ {\left( {{d_{t + 1 + j}} - w_{t + 1}^*} \right) + \beta \left( {1 - s} \right)A_{t + 1 + j + 1}^J\left( {w_{t + 1 + j + 1}^*} \right)} \right]} \hfill \\
=& \left( {{d_t} - w_t^*} \right) \\
&+ \beta \left( {1 - s} \right)A_{t + 1}^J\left( {w_{t + 1}^*} \right) + \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]\sum\limits_{j = 0}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}{E_t}\left[ {\left( {w_{t + 1}^* - w_t^*} \right)} \right]} \hfill \\
&+ \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]{E_t}A_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
=& \left( {{d_t} - w_t^*} \right) + \beta \left( {1 - s} \right)E_tA_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
&+ {E_t}\left[ {\left( {w_{t + 1}^* - w_t^*} \right)} \right]\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]\sum\limits_{j = 0}^\infty {{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}^j}} \hfill \\
&+ \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]{E_t}A_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
=& \left( {{d_t} - w_t^*} \right) + \beta \left( {1 - s} \right)E_tA_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
&+ {E_t}\left[ {\left( {w_{t + 1}^* - w_t^*} \right)} \right]\frac{{\left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}}{{1 - \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]}} \hfill \\
&+ \left[ {\beta \left( {1 - s} \right)\left( {1 - \gamma } \right)} \right]{E_t}A_{t + 1}^J\left( {w_{t + 1}^*} \right) \hfill \\
\end{align}