Hello everyone
I am working on a small open economy model based on Adolfson et al (2007) but a non-linear version with some simplifications (no consumption habits, no capital utilization costs and no wage rigidities). My plan is to do a welfare analysis once I have estimated some parameters with data, however, in the last few weeks I’ve had a problem for which I would greatly appreciate if someone could help me with any suggestions or comments.
When I simulate the model with zero inflation in the steady state (\Pi = 1) I have no problem and the model runs fine, however, when I assume a positive inflation rate in the steady state the model becomes very sensitive to the calvo parameter of price rigidities (\theta), and I only meet the BK conditions when \theta is low enough, for example, when \Pi = 1.01, \theta needs to be less than 0.76, otherwise i get: Blanchard & Kahn conditions are not satisfied: indeterminacy. The model only admits larger values for \theta as long as the Taylor rule inflation reaction coefficient (\phi_{\Pi}) increases. At first, I thought it was a feature of the model, but now I think it is some kind of mistake, which I have not been able to detect.
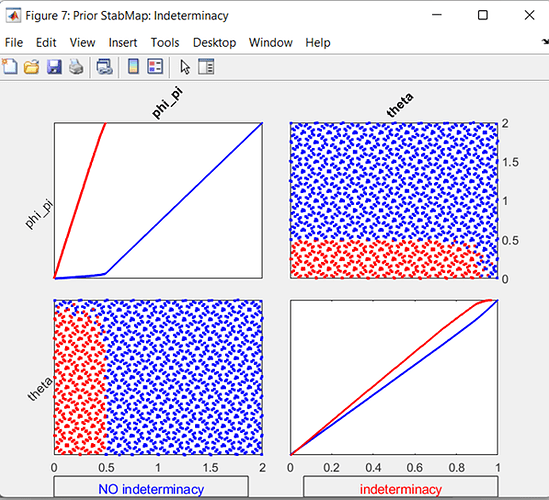
To further analyze this problem, I did some basic sensitivity analysis. When \Pi = 1 and analyzing together \theta, \phi_{\Pi} and \phi_Y I get the following plots:
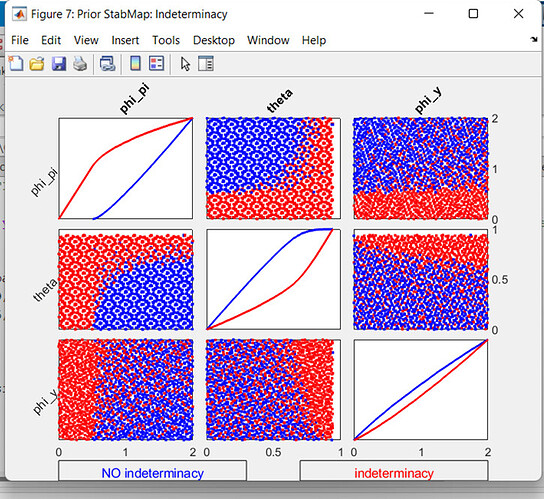
Which are consistent with the Taylor principle and allow for greater values of \theta, however as soon as I set the inflation in the steady state to a positive value, say \Pi = 1.01, I get the following:
The permissible values of \theta do not exceed 0.7 and the central bank’s reaction parameter to output (\phi_Y) begins to be problematic as well, with many values that generate indeterminacy (situation that did not occur when \Pi = 1). My thoughts is that it is a mistake rather than a feature of the model. Since my goal is to analyze the optimal parameters of the Taylor rule in a positive inflation scenario, this is giving me some problems. If anyone has faced a similar situation, or if someone with more experience can tell where the problem may be, I would greatly appreciate your comments. I attached the MOD file.
Greetings and thanks in advance
Eduardo.
SOE_org_pf.mod (19.4 KB)