Dear Dynare Team,
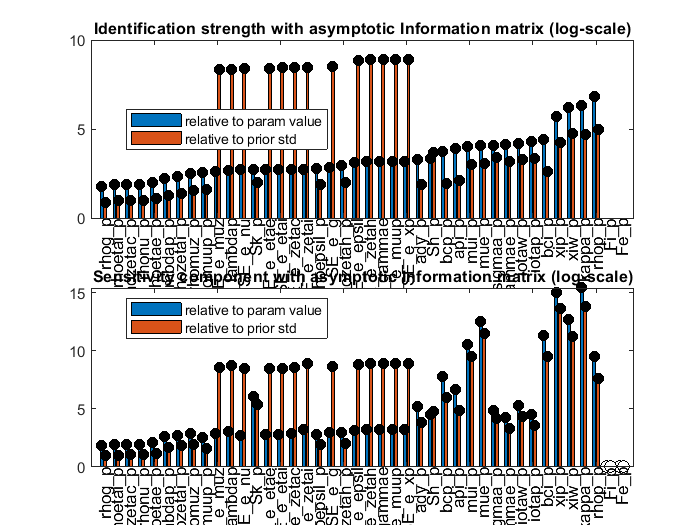
I have a question regarding identification issues in my model. I am currently trying to replicate the model from the paper “Collateral Shocks” of Yvan Becard and David Gauthier by estimating it for Germany. The major problem that I am facing is that in the original code of the authors, the authors estimate two steady-state default probabilities, those of impatient households that invest in housing and those of enterpreneurs. Now, if I run a simple identification check, the sensitivity analysis tells me that these parameters are fundamentally not identified (see Fe_p and Fi_p in the attached attached graph), as the sensititivity with regard to these parameters is 0.
If I am not mistaken, this should, among other things, lead to problems with the mode-finder. Nevertheless, if I feed the model with the respective data, the mode can be easily computed (using mode_finder = 5). Furthermore, the mode check_plots indicate that the likelihood and the posterior have a distinct peak at the mode. On top of that, if I run an MH-algorithm, the posterior is very distinct from the prior in both cases, which further contradicts the unidentifiability of the paramter.
Ultimately, if I make a simple a comparison between two model specifications in which I keep everything constant, except for the two steady-state default probabilities, the theoretical moments of the observable variables in my model change significantly. Given the identification method of Iskrev (2010), this should not be the case if the parameter is unidentifiable, as if a parameter is unidentifiable, it should not influence the moments of the observables, right ?
Now, my question is, am I missing something or does the identification command potentially give me a wrong result in this case ? It might be worth noting, that to compute the steady-state, I use a seperate matlab file. Maybe this creates an issue with the identifcation tool ?
I would greatly appreciate any help, as this question keeps puzzeling me.