How to explain IRFs

Stochastic simulations
1

Hi all,

I have a series of questions about IRFs. Maybe, they are basic questions but I have not found answers yet. Any help is very well appreciated! Thanks!

Q1.
Should we always interpret IRFs using solely the equilibrium equations of our model or we can mix that with economic intuition (that may not be explicitly captured by the equilibrium equations of our model).

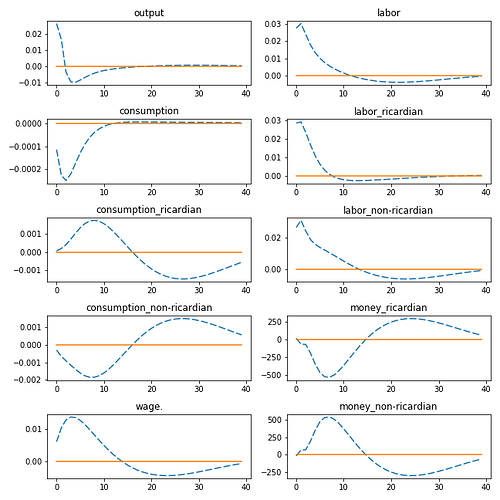
For example, from the equilibrium equations of a simple RBC model (with only ricardian households), an increase in aggregate labor supply and aggregate consumption (after a productivity shock) is well captured by the equilibrium equations of the model, and this is also seen in the IRFs.

In complex models (with both ricardian and non ricardian households), however, Celso Jose Costa Junior (chapters 6 and 7) explains that the response of aggregate labor supply and aggregate consumption (to productivity shock) depends on income and substitution effects as ricardian and non-ricardian households respond differently (in an opposite fashion). Ricardian households increase labor supply and reduce consumption. Non-ricardian households, on the other, reduce labor supply and increase consumption. On aggregate, labor supply falls, and aggregate consumption increases (which is in contrast to simpler models (chapters 2 and 3) with only ricardian households where both aggregate consumption and aggregate labor supply increases after a productivity shock).

While the IRF explanations in the book make sense, income and substitution effects are not explicitly captured by the equilibrium equations of the model. In this case, it appears to be more of an economic intuition to help explain the IRFs. Thus, why ricardian and non ricardian households respond differently to productivity shock.

So it is not like, ricardian households will always reduce consumption (chapters 6 and 7) or increase consumption (chapters 2, 3, 4) after a productivity shock (see, Junior, C. J. C. (2016))

Given the above, my understanding is that, if we can find sound economic intuition to help explain the IRFs, then we are fine even though that intuition may not be strictly captured by the equilibrium equations of our model (for example income and substitution effects). Nevertheless, some IRFs like output response to productivity shock is kinda standard, I guess.

Q2.
Here is my 2nd question. Given that aggregate labor and aggregate consumption (among others) may go either way after a productivity shock (for example, in models with ricardian and non-ricardian households), should we change values of structural parameters or adapt our model in a way such that the model is consistent with the economy we are trying to build the model for? In relation to my first question, this will be, for example, by adjusting the proportion of ricardian and non-ricardian households depending on whether we want a procyclical aggregate labor supply or a countercyclical aggregate labor supply after a productivity shock.

I am sorry for such a long question.

2
  1. Income and substitution effect are embedded in the preferences of the agent and enter e.g. via the Euler equation. Thus, they are present in the FOCs, even if you cannot immediately read them off. They are what explains why the FOCs give rise to the responses you observe. So there is no contradiction here.
  2. Usually yes. If your goal is build a model economy to mimic an actual economy in order to conduct thought experiments or counterfactuals, then that model economy should mirror the behavior of the actual economy. That usually involves assigning parameter values in a particular way.
3

Hi Prof. Jpfeifer,

Thanks for the reply!!

4

final
final648×648 43.2 KB

Hi Prof. Pfeifer,

When you have the time, could you kindly comment on my explanation of the IRF for consumption (with regard to a productivity shock)? Many thanks!!!

Regarding consumption, non-ricardian households decrease their consumption in the initial periods and instead increase their money demand holdings. Since these households face credit constraints and are unable to borrow or save to smooth their consumption, carrying money to the next period seems to be a feasible alternative. Ricardian households, on the other hand, increase their consumption in the initial periods while decreasing their money demand holdings (i.e., the amount of money they carry to the next period). This is due to the fact that they have the opportunity to borrow to smooth their consumption in all periods. On aggregate, total consumption falls in the initial periods before increasing gradually to the steady-state level.

1 Like
5

That story is consistent with the pictures show, but only you as the model builder can judge whether it is indeed correct.