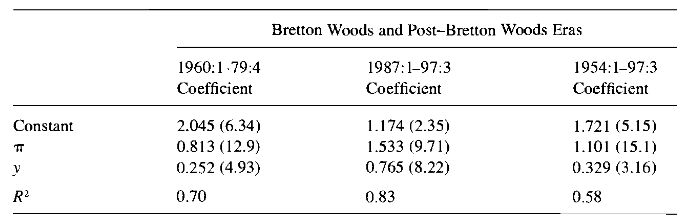
Taylor (1999) checks whether the Taylor principle is satisfied in historical data for specific periods by estimating his proposed rule (the original rule). For 1987:1-1997:3, for example, the Taylor principle is satisfied.
But if we extend the original Taylor rule to include other variables and allow for interest rate smoothing, the coefficient on
\pi may not be greater than one.
In the empirical literature, others have used different specifications of the central bank’s reaction function to make similar statements like, “the Taylor principle is satisfied for period A.” But, of course, it depends on the model. I tried to say somewhere that the Taylor principle is satisfied for some period for my country based on an estimation of the original rule…similar to the table above. But one comment I got was that it is not satisfied because, in other specifications (allowing for lags and other variables) that I also showed, the coefficient on \pi is less than 1. So it seems we cannot really make a general statement that “the Taylor principle” is satisfied for some period, right? Like there is no consensus on a specific empirical model that one should use to answer whether or not the Taylor principle is satisfied, it seems. I guess the best answer is it depends (on the model).
In the Taylor paper, he mentioned, “I abstract from lags…”. And sure, others will specify the rule differently from the original rule. Is it fair to say that there cannot be a definite answer or consensus on whether the Taylor principle is satisfied for some period? Here, I mean in empirical models, not structural models.
It’s not even clear you can estimate the Taylor rule outside of a structural model. That is a point forcefully made by Cochrane (2011) in the JPE.
But yes, all model estimates are dependent on the model and the data may not be informative to select between models. You will never be able to test all the potential models that people may put prior mass on.
1 Like
Dear Prof. Pfeifer, may I ask this question if I may? So in Cochrane (2011), if I understand, he is kind of saying that we cannot really call Taylor’s proposal (of raising the interest rate more than one-to-one to changes in the inflation rate) as indicating determinacy if we estimate the Taylor rule using regression (i.e., outside of a structural model with rational expectations). I think I understand his argument. Like, in an adaptive expectations model, the inflation rate may still explode rather than stabilize even if the central bank raises the interest rate more than one-to-one to changes in the inflation rate…and the inflation rate may stabilize rather than explode even if the central bank raises the interest rate less than one-to-one to changes in the inflation rate.
So it seems there is no way to check whether the central bank moved from an indeterminate regime to a determinate regime, right? Thus, either using a model with rational or adaptive expectations. But at least, in the 1980s, we can say that the central bank became more hawkish, right? Like, we don’t know if it moved from an indeterminate regime to a determinate regime, but we can say for sure that the central bank became more hawkish, right?
I recently heard Cochrane asking whether the Fed should repeat the 1980s with respect to the current inflation situation in the US. And then he said no, there is a better way, and then talked about his fiscal theory of the price level. So I guess he is acknowledging that the Fed indeed raised the interest rate to stabilize the inflation rate in the 1980s, but that it cannot be called a movement from indeterminacy to determinacy, right?
No, Cochrane’s point there is that you cannot correctly identify the off-equilibrium behavior of the central bank described in the Taylor rule by only equilibrium observations without a model. For the intuition, see Worthwhile Canadian Initiative: Why are (almost all) economists unaware of Milton Friedman's thermostat?
1 Like