I have a general question about DSGE models. In Gali’s books, he provides the SVAR model below as evidence for abandoning the classical monetary model for the New Keynesian model.
What if there is lack of this evidence for some economy? Say, after a tightening of monetary policy in an SVAR model, the responses of both inflation and real GDP are insignificantly for economy A. Meaning,
- The weak inflation response can be interpreted as evidence for price stickiness.
- But at the same time, the weak response of real GDP can be interpreted as no strong real effects.
When empirical evidence does not fit the prediction of the model, can one go ahead and use the model anyway for policy analysis? For example, the CB in my country has a QPM model for policy analysis but the predictions of that model is not what one sees in the data, even qualitatively.
I am confused and wondering when is empirical evidence relevant in macro and when it is not. Can belief, for example, replace empirical evidence? Like, can I say, it is my belief that monetary policy have real effects in economy A, so although I have no evidence for it in the data, I am still gonna use this model consistent with that belief?
And even in Gali, the empirical evidence is for four variables, but the model contains way more variables. In DSGE modeling, can one ignore evidence for other variables and just focus on a few variables one is interested in? These are questions I have but have not found answers in textbooks.
I think there is ample evidence that money is not completely neutral. That suggests using a NK model. However, the strength of this effect is mostly a matter of parameterization. In the limit of no price stickiness, you will get the RBC model. For that reason, pretty much all central banks estimate their model using likelihood based techniques. That approach forces the model to explain the comovement of all observed data. The parameters should then reflect your findings.
1 Like
My understanding of your statement above is something like, ‘the effect of a monetary policy shock is not completely zero, even if it is statistically insignificant’. Is that a right way to think about it? So that even if the empirical responses are not statistically significant, we can still estimate NK model for policy analysis.
Is the statement above why I have the following results?
- Using initial prior values to simulate my model, interest rate increases and inflation and output fall following a monetary tightening.
- However, for the estimated IRFs (using Bayesian methods), all three variables fall following a monetary policy tightening. Is it because the comovement between these three variables is positive in the data, and that the estimated model is capturing that positive comovement ?
Hi Prof. Pfeifer, thanks for the response. That reminds me of another question that I have which is a little related.
The moments from the model after estimation or simulation are conditional moments, right? So we cannot really compare that to the unconditional moments computed straightaway from the data (like taking correlations and variances of observable variables). May I ask if
- whether it is necessary to compare model moments to data moments after estimation?
- And if yes, what kind of data moments?
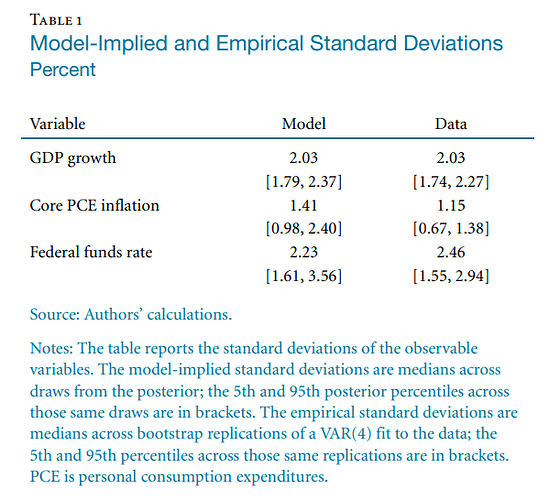
In one DSGE paper, “Policy Analysis Using DSGE Models: An Introduction”, the authors compare model moments to data moments, where data moments are “medians across bootstrap replications of a VAR(4) fit to the data”.
I do not know what “bootstrap replications of a VAR(4) fit to the data” means yet, but are the authors doing this because they want to compare conditional moments from the DSGE model to some sort of conditional moments from the VAR model? Like they can not just compare conditional moments from the model with unconditional moments from the data (by just taking moments of observable variables), right?
I am not sure I am following. The moments from the model and the data are unconditional moments, i.e. after all shocks occurring in the sample/model happened. Conditional moments would be after a particular identified shock.
Usually, a VAR is not needed for the comparison of unconditional moments. It seems the VAR is only needed here to get confidence bands on the data moments.
1 Like
I see, thanks. I understand now. I was using ‘unconditional’ wrongly. I thought moments from the model (even after all shocks occurred) were conditional…that is conditional on the shocks in the model.
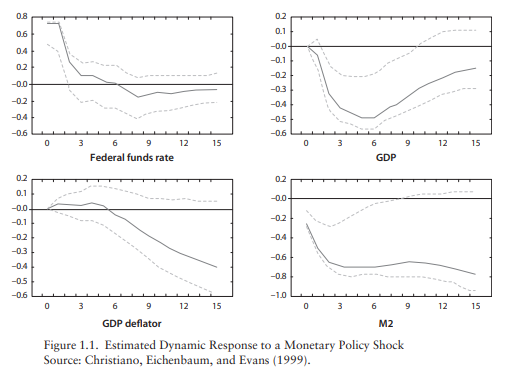
Dear prof. Pfeifer, may I revisit this comment? I understand it, and in the figure I posted earlier from Gali’s book, for example, the fall in GDP is statistically significant following a monetary policy shock. However, if you look at the GDP deflator in the figure, it is statistically insignificant for all periods after the shock…but Gali seems to use that later decline in the GDP deflator after a few quarters as evidence for a fall in price following a monetary policy shock. Are qualitative properties of VAR IRFs enough as evidence in macro modeling even if they are not statistically significantly different from zero? Like why did he not instead develop a model where the price does not respond at all following a monetary policy shock? He may be using economic significance instead of statistical significance here? Or maybe when it comes to evidence from a VAR, qualitative properties of the IRFs are enough? Would love your comment on this.
Most monetary VARs show a delayed response of prices. That’s not something the most basic New Keynesian model can replicate. But more sophisticated medium-scale models are able to match the empirical evidence. A prime example would be the Christiano/Eichenbaum/Evans (2005) paper.
1 Like