How are model IRFs matched with VAR IRFs?

Estimation SMM/GMM/IRF-Matching
1

Hi everyone,
I know IRF matching is to minimize the distance between the model IRFs and empirical IRFs.
But model IRFs are driven by exogenous shock while empirical IRFs are driven by shocks to a variable.
The shocks are different. How do I match them?
Is the technology shock in model equivalent to a shock to Y in VAR?

2

Hi,

I am not familiar with the approach… But I suppose that in the VAR, to obtain what you call ‘‘empirical IRF’’, you do not just hit an exogenous variable… You must have an identification scheme. The identification scheme you consider is different, a priori, from the one embodied in a DSGE model (which comes with more restrictions than the VAR model). But the game is to minimize the gap between the identification schemes by adjusting the values of the DSGE’s parameters.

You may obtain more informations in this thread DSGE based-on IRF from VAR's.

Best,
Stéphane.

3

Exactly, IRF-matching works with a structural VAR (sVAR), not a reduced form one.
An example is at

4

What about if one tries to match the conditionnal variances rather than the IRF point estimates of the SVAR ? when I try to modify the objective function minimized in your example by including moment conditions on conditionnal variances, for example : var(y_model) - var(y_target), where var(y_model) is the variance of y of the theoretical DSGE model we estimate, and var(y_target) is the conditionnal variance found through the empirical SVAR (a given fixed value), the program does not work (I use for instance diag(oo_.var)…)

Can someone please help ?

5

You set

options_.nomoments=1;

which shuts off the computation of moments. That cannot work.

6

Oups !

Ok thanks !!

:slight_smile:

7

Hi

I have a related question. IRFs from the emprical model (VAR) starts from zero value (I do not mean Period zero) but when we get IRFs from the model (Theoretical IRFs), Dynare does not start them from zero values. Is there anyway to have both emprical and theoretical IRFs start from zero values.

Thanks in advance for your help

8

What do you mean with “starts from zero value”? Did you restrict the VAR to not have impact responses? Or does the timing not match?

9

dynare
dynare1702×762 220 KB

Thanks for your reply.
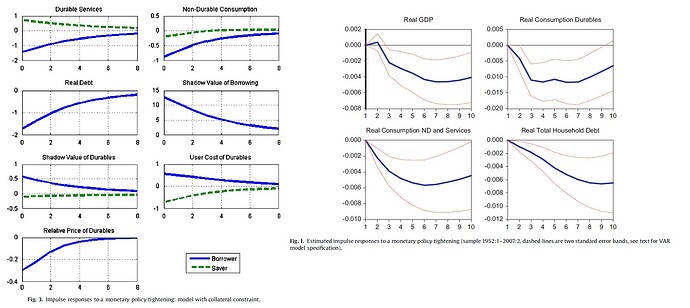
For example, if you see Monacelli’s 2009 paper; you can see all the emprical IRFs from the VAR model starts from zero and then you can observe the dynamics greater or less than zeros for periods 1, 2 , … , etc. But when you check the results from the model, IRFs have positive or negative values at time zero (or even period 1) when the dynamics start. My question is, what is the reseason behind these IRFs that causes to see different values at the starting point.

10

That picture looks like a monetary VAR where impact responses are restricted. To get something like this in your model, you either need a particular information structure or a lot of endogenous frictions like adjustment costs.

11

Thanks a lot for the useful comment. I am familiar with the adjustment costs and the way they affect the model. However, could you please explain more about the information structure you mentioned. How can I consider that in the model?
In lot of papers I’ve seen, this problem (if we can call it a problem) exsits. Do you think it is an important issue if someone wants to use the results from a VAR model and compare them with the dynamics obtained from the theoretical model?

12

See e.g.

and the reference therein. And yes, it is important that the assumptions in the model and the VAR match.