Homotopy calibration

Macro-language
#1

Hello everyone

I’ve been working in Eichenbaum, Rebelo and Trabandt (2020) model. They solve a macro-sir model in both, neoclassical and NK context. But I have lots of questions about their dynare code.

  1. They solve the non linear model by using homotopy. What does it mean?
  2. Why they use “format long;” in the parameters section?
  3. How does work “go_calibrate_pi;”?
  4. It would be possible run the code by separating neoclassical model from the NK model?

Thank you so much. The code is attached below. ert_model.mod (17.2 KB)

#2
  1. Homotopy solves the full problem by first solving a problem with a smaller shock and then using this solution as the starting point for the next, bigger step.
  2. format long is a Matlab command for having output displayed with more digits.
  3. You did not provide the code.
  4. Yes, if you can identify the respective equations and variables.
1 Like
#3

Thank you for your response, Professor Pfeifer

My doubts has been resolved successfully. In regard to the third point, this is the code: go_calibrate_pi.m (791 Bytes)

Finally I could separate the necolcassical model from the neokeynesian model and also, I introduced a consumption tax shock. The model response, partialy, in the way that I have expected:

  1. The consuption has reduced in response of an increase in the consuption tax.
  2. Thus, the investment and capital increase.
  3. In theory, the number of infected population sould be reduced, since the interecations between susceptible and infected people is lower. But this didn’t happen in the simulation. What would be the reason and how can I solve this problem?
  4. The inflation rate increase, when it would decrease. Why does it happen?

This is the model with a increase of taxes: macro_sir.mod (9.7 KB)

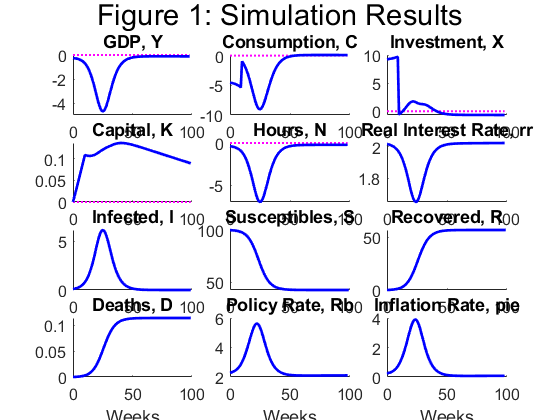
Tax shock

An this is the original model: ert_model.mod (17.2 KB)

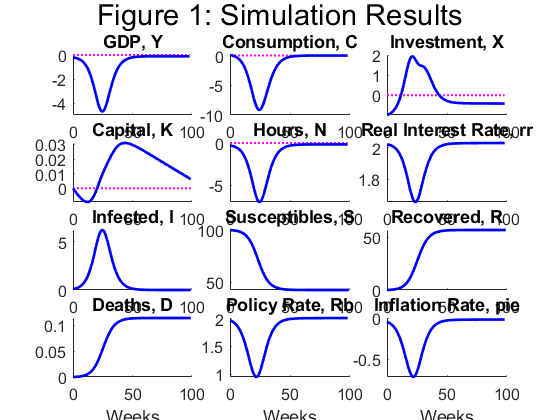
Normal

Thank you so much!

#4

These are questions where users will typically not be able to help you. You are the model builder and need to understand what is going on in your model.

#5

Hello!

I’ve been working in ERT (2020b) model too. But I was unable to successfully replicate it like the original because errors below.

Not enough input arguments.

Error in sim1 (line 33)
verbose = options.verbosity && ~options.noprint;

Error in ert_model.driver (line 949)
sim1;

Error in dynare (line 293)
evalin(‘base’,[fname ‘.driver’]) ;

Please help me to fix it.
I use Matlab version 2020b and Dynare 4.6.3.

Thank you very much.

#6

You most probably have a problem with the Dynare version. See How to set a lower bound at version 4.4.3?

#7

Thank you so much, Professor!
I can run it without error.