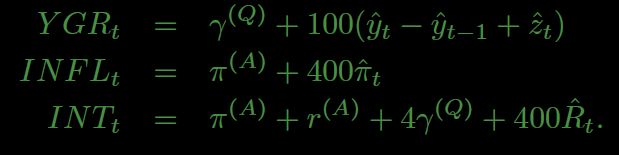In a state-space representation, the measurement equation is something of this form O_t=H_t s_t+u_t, where O_t are the observational data at time t, H_t is a possibly time-dependent matrix relating the state s_t and the observational data. We can see u_t as the measurement errors at time t.
However, in Herbst and Schorfheide book (Bayesian estimation of DSGE models),
we have s_t dependent on y_t, but not y_{t−1}, while the measurement equations are of the form:
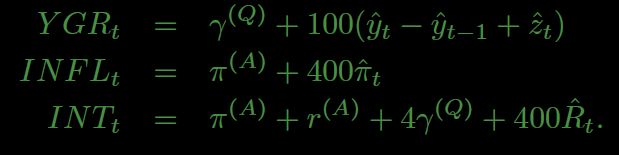
Is this a typo? Should I add the y_{t−1} term to s_t?
To which page of the book are you referring? I also do not understand what you mean with
Do you mean the lag of \hat y_t, i.e. \hat y_{t-1}, showing up in the measurement equation above? If that is the case, then you forgot that \hat y_{t-1} is part of the state vector s_t, because at time t, it cannot be changed anymore.
Dear Jpfeifer,
I’m referring to the measurement equations on page 19 of the book.
Also, the way the state-vector was defined, for the model under consideration, is in page 16. In the definition \hat y_{t-1} does not belong to s_t…
s_t in the book is not the state vector, but a collection of all variables in the model. Moreover, s_t was defined before the observation equations were introduced. You are right that there is an inconsistency and one would need to define s_t appropriately to include \hat y_{t-1} for the generic observation equation for y_t to be correct.
Dear jpfeifer,
To be sure, you’re saying that the s_t solving the model, is not necessarily the same s_t for the state-space representation?
Any help would be appreciated.
No, the observations equations are part of the model. But the way the book proceeds, s_t is defined for the model without the observation equations. Then, after the observation equations are defined, s_t is used in a generic way not compatible with the previous explicit definition where y_{t-1} did not show up.
Ok. Thanks Jpfeifer, for all the help.