I’m a new Dynare user trying to graph the transition path to steady state for consumption and capital for the model below.
var c, k, y;
parameters alpha, beta, delta, TFP;
alpha = 0.36;
beta = 0.99;
delta = 0.025;
TFP = 1;
model;
c(+1) = beta*c*(TFP*alpha*k^(alpha-1) + (1-delta));
k = TFP*k(-1)^alpha - c + (1-delta)*k(-1);
y = TFP*k(-1)^alpha;
end;
initval;
c = 1;
k = 1;
end;
endval;
c = 1;
k = 1;
end;
steady;
simul(periods = 500);
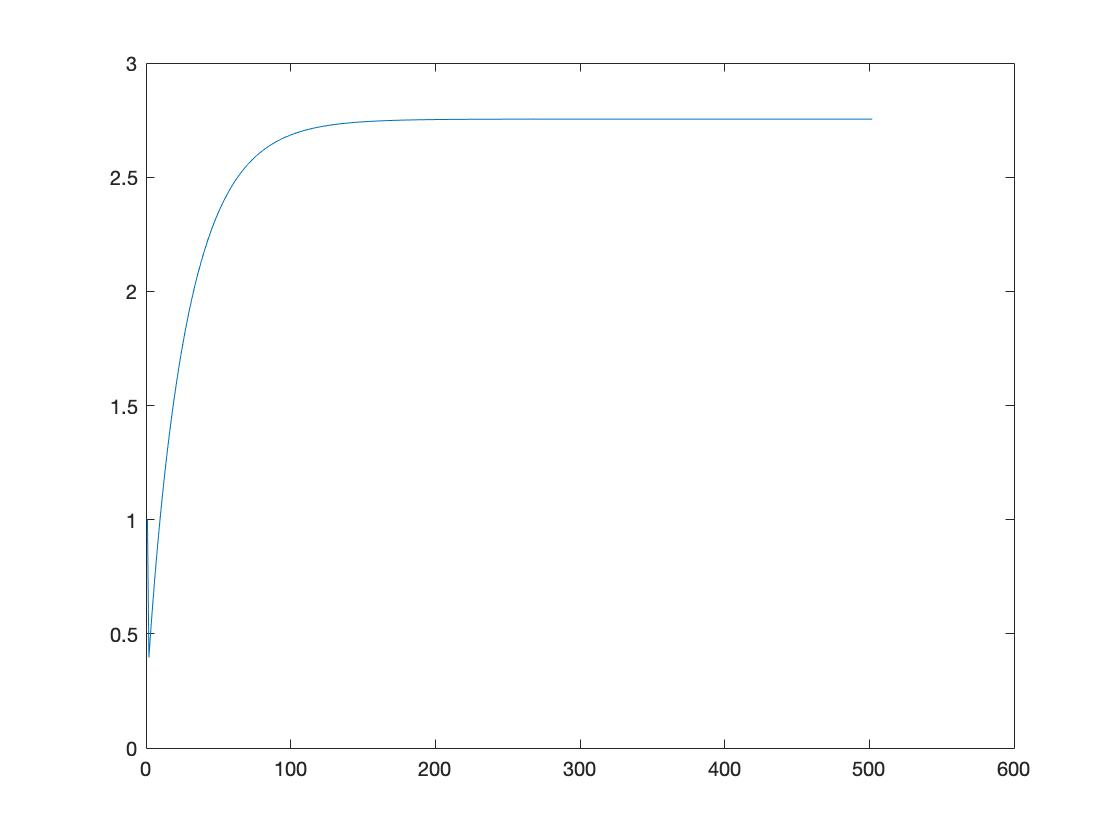
As you can see, it a simple Solow model. When I plot consumption after running it, I expect to see a smooth concave function. Instead, I find that my consumption first drops below 1.00 and then slowly goes up to steady state (see attached graph) - which should not be happening. Any pointers as to how I can make sure this does not happen? I do get the right steady state results though.
Dear p_geethika,
I set an endval equal to the steady state and an initval not too far from it. Chek it if it works now.
Best,
Valerio
solow.mod (366 Bytes)
Indeed, consumption is not predetermined. So the first value shown is meaningless as it corresponds to the value you set. It is not endogenously computed.
My issue is not with the first value set - it is what happens during the first time period (t=1). Why does consumption fall below one first and then go up to steady state? As per my understanding, this should not be happening. If consumption falls below one, then the utility associated with consumption in this model (given that U = log©) will become negative. That doesn’t make sense to me - any pointers on why this may be happening?
My understanding is the following. In period 1 consumption is equal to the value that you define in initval: you can set it to 1, 20, 200, it does not matter because consumption is not predetermined. What it is important is the initval of k, which is going to affect period 2 consumption and period 2 capital. Try to set the initval of c to 100 (keeping the initval of k to 1): you will see that period 2 consumption is still 0.3964.
True, if c<1 utility is negative, but it does matter: the utility function just ranks different allocations and its value is meaningless per se. If you set U=100000+logC, utility will never be negative, but the model will be isomorphic to a model with U=logC.
Valerio
1 Like