Hello everyone:
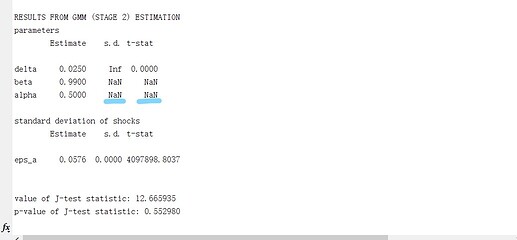
I’m trying to use GMM to estimate nonlinear SOE model which refers to Prof Pfeifer . And the estimated alpha(capital share)、beta、delta show “NAN”, I would like to know what is the reason for this.
And about GMM estimation, I have two questions:
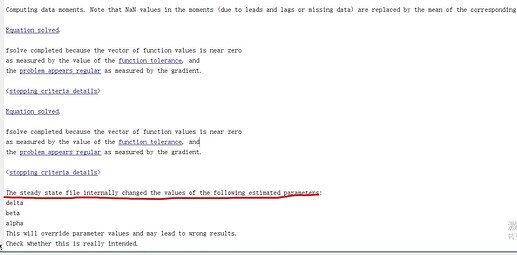
(1) I use steady-state.m to solve the mod, and GMM hints that the estimated parameters may have an effect on the steady state, is this information prompt normal?
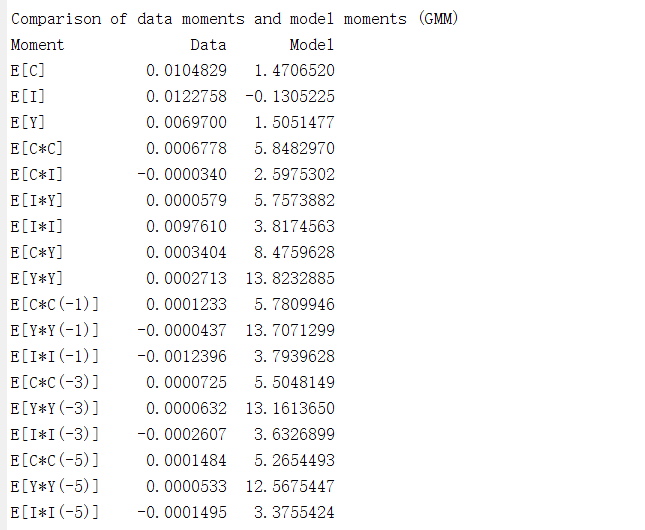
(2)About varobs variables, in my model, I choose C Y I, and the estimation results show that the moments of the model and the data are very different.
I’m really confuse that how to choose varobs variables, consumption investment、output、employment、inflation、, these variables can be obtained from the data. So which variable should we use? or could I choose any one?
Thanks for all in advance.
Your Results from GMM (Stage 2) Estimation indicate that delta, beta and alpha are still at their initial values (0.025,0.99,0.5), which is very weird and points towards some dependent parameter problem. eps_a seems to change, but looking at the standard error and the comparision of data and model moments this is not a reliable estimation. You do have parameter dependency problems in your model. This seems to be supported by your steady-state.m file as these parameters change their value during the steady-state computations; why is this the case? Do you really want to estimate these parameters or actually other parameters? Have you done an identification analysis?
Without seeing the codes, I think there is something wrong in your steady-state file. Only if you fix this first, then you can have a look at the comparison of data moments and model moments and try out different varobs and moment conditions. Which variables you should use again depends on your model and the parameters you are interested in. The identification and global sensitivity toolbox of Dynare can help you guide towards finding observables that are useful for estimating certain parameters, but in the end this is a bit of a trial and error task, there is no general guidance.
Thanks for your patient reply, Prof Mutschler.
I have learned again today what you taught about identification and GMM/SMM in summer school . It really helped me understand the problem. Thank you so much!
I have tried to estimated parameters in third order nonlinear model with uncertainty shock. The result is still weird. I have two questions:
(1) About identification at order 3
In your summer school lecture, you mentioned that the identification at order 3 can only be done with Kalman filter or Particle filter. But in Dynare manual release 5.0, it mentioned identification at order 3 can be done with pruning:
So I introduce identification(order=3,parameter_set=calibration)to mod file, it report:
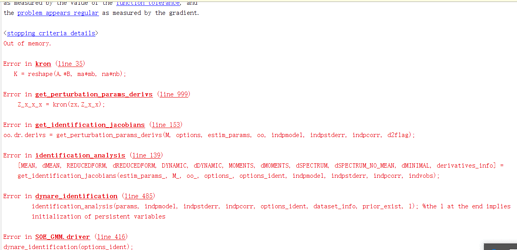
Out of memory
Error in kron (line 35)
K = reshape(A.*B, ma*mb, na*nb);
But if I introduce identification(order=2,parameter_set=calibration), identification analysis runs well.
Which cause the identification at order 3 errors? Prof Mutschler.
(2) About GMM at order 3
The estimation is also weird, And I would like to estimate rho_tau, rho_sigma_tau,sigma_tau_bar, sigma_sigma_tau at third order, the result is also weird. I write mod file referring to RBC_MoM_GMM.mod
(3)About SMM at order
I have tried estimate these parameters by SMM, but it also report:
I sent my files via P.M, thank you so much, Prof Mutschler.
@Jingjing Can you also send me the files?
The out of memory message suggests your model is too big for your machine to run the code. Also not that if identification works at lower order, it should still hold at higher order.
I sent the file via P.M, Thank you very much,Prof Pfeifer.
Thanks for your patient reply, Prof Pfeifer.
I have two more questions about SMM:
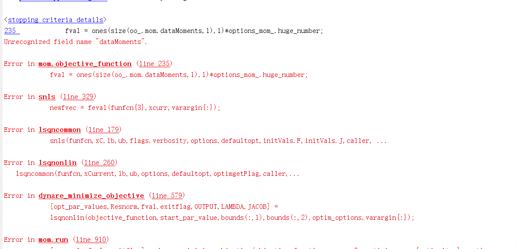
(1) I think there is a bug in line 233.
I change two line in objective_function.m, but when I run the SOE_SMM.mod, it report:
and I pause the objective_function.m in line 232,
So I change the line 233 in objective_function.m:
fval = ones(size(oo_.mom.data_moments,1),1)*options_mom_.huge_number;
The mod file can run sucessfully.
(2) I think there is something wrong with my data or code, but I really don’t know where is wrong.
When I run the nonlinear model at order 3, the result is weird:
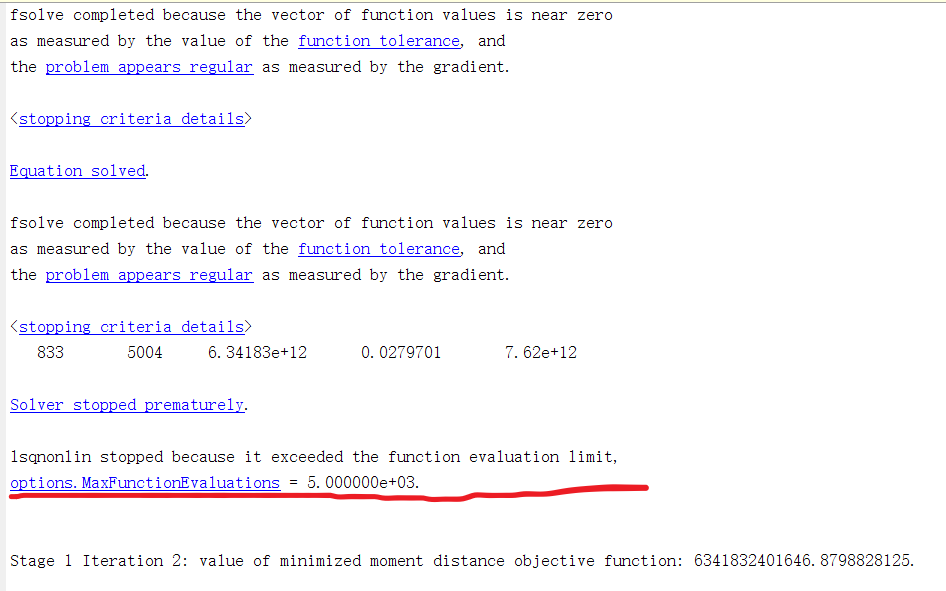
Figure 1 show lsqnonlin may be not solve the problem?
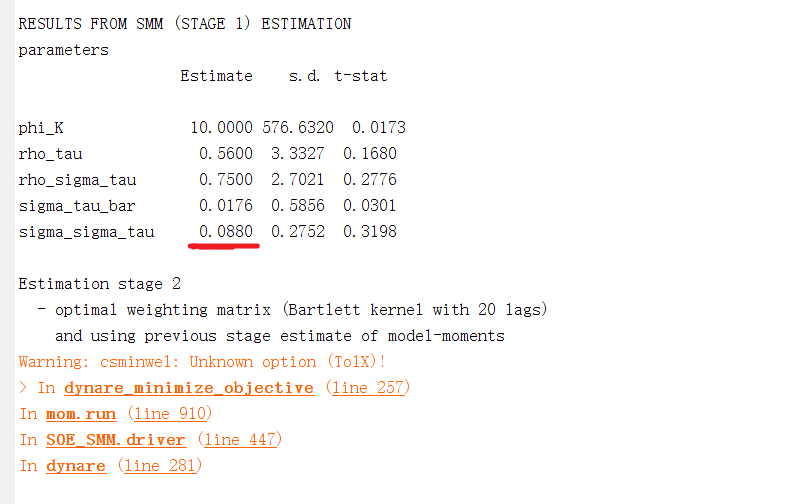
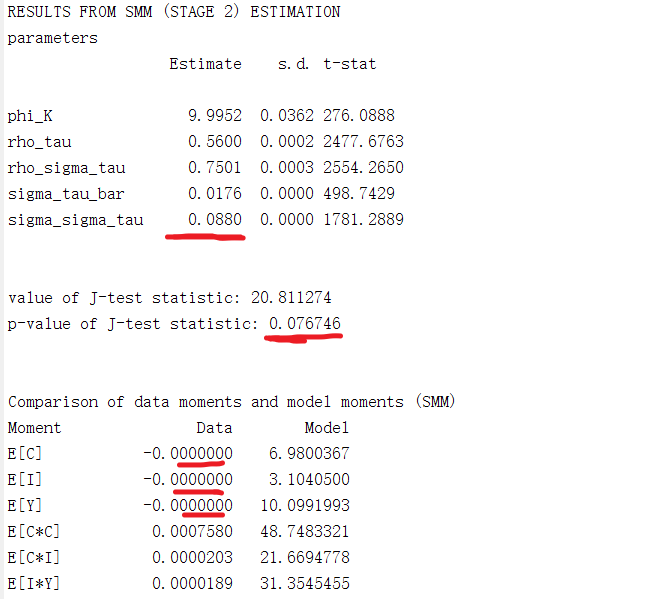
Figure 2 and 3 show estimation at stage 1 and stage 2 is close, and I think the value of J-test is wrong.
Data moment :E(C) E(Y) E(I) is 0.0000
As you can see, I think the mod file and steady_state.m are right, because my model only introduce uncertatiny shock into Gali chanpter8 nonlinear model.
And I use hpfilter process data, so it is stationary.
but the result is really weird.
Hello, Prof Pfeifer.
I have another question to trouble you about SMM estimation.
I would like to estimate alppha, varphi, upsilon, eta_g in nonlinear model at 3 order,(the operation is still in the previous mod file )
estimated_params;
alppha, 0.5212;
upsilon, 0.4;
varphi, 5;
eta_g, 2;
end;
These parameters meet the identification conditions,but it gives erro:
I try change the name of parameters, like alppha_g, varphi_g, upsilon_g, but it still reports the above error.
Thanks for your help, Prof Pfeifer.
Could you please provide me with the file to replicate the issue?
I sent the file via P.M, Thank you very much,Prof Pfeifer.
Thanks, I am looking into it.
Hi,Prof Pfeifer.
Have you found a new reason for this problem?
I’ve only been trying for a few days, but I still get an error about estimating alpha、varphi.
Thanks for your help sincerely!
Hi, Prof Pfeifer, All the code works,Thanks for your help sincerely!
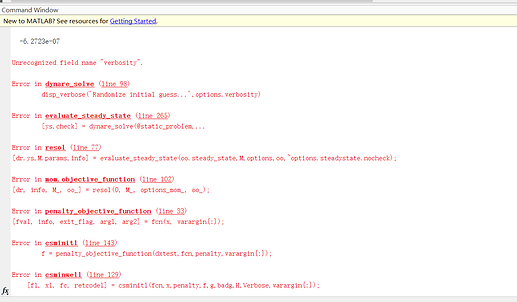
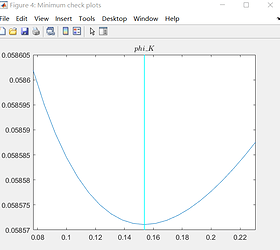
The following two errors have occurred in dynare,
(1)
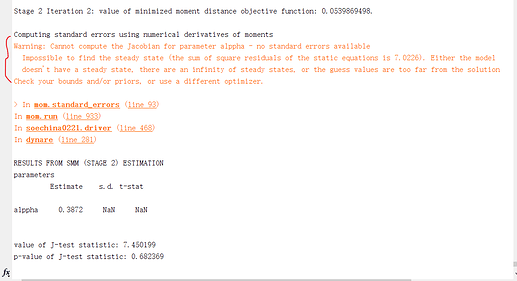
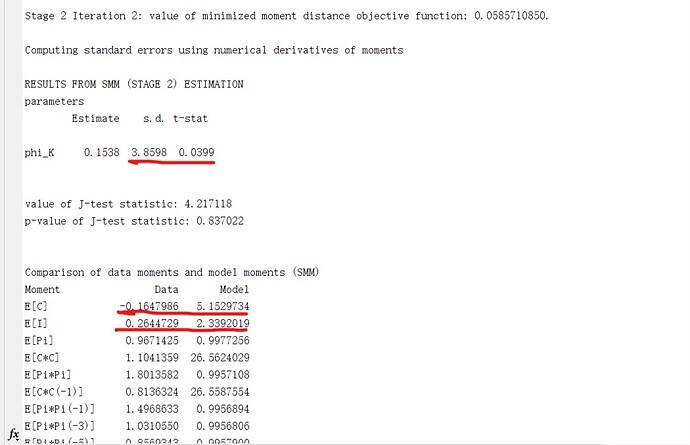
(2) the s.d of estimation parameters is high, but t-stat is small, and there is mismatch between data moments and model moments.
(all data divided by the GDP deflator and population, then log-transformed and detrended using the HP-filter,expection for inflation)
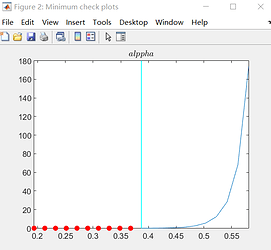
The first error comes from the numerical derivate not being computed to the steady state computation failing. You can see this in the red dot. The low t-state reflects the large standard error relative to the mean. You cannot reject the parameter to be 0.
Thanks for your reply, Prof Pfeifer.
For low t-stat and large distance between data moments and model moments, do they suggest that my observed variables is not good? or model is wrong?
If I would like to improve this problem, I need to re-find suitable observed variables and matched moments.
Thanks!
I am a bit puzzled by the means being so different. So maybe the observation equation is wrong.