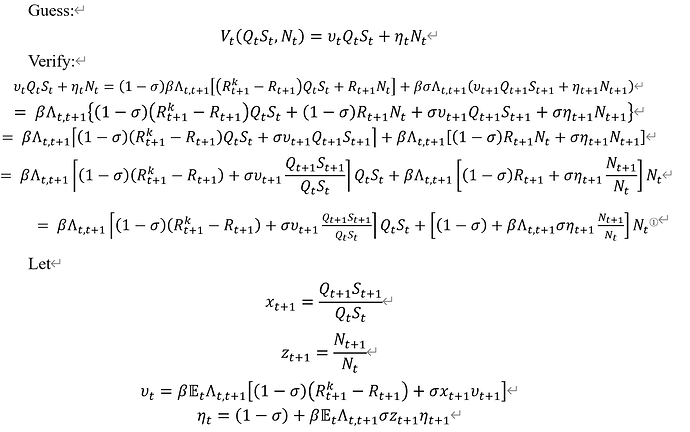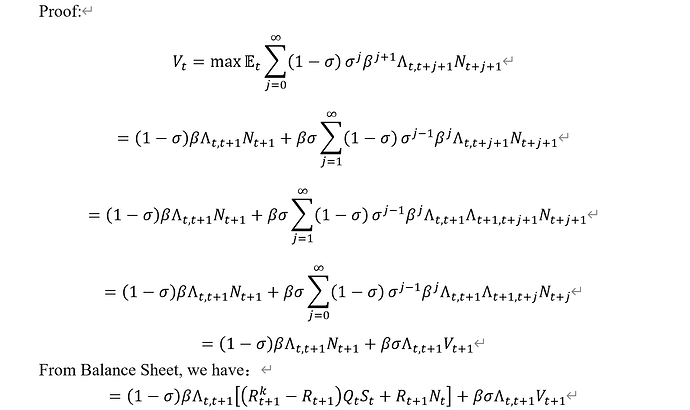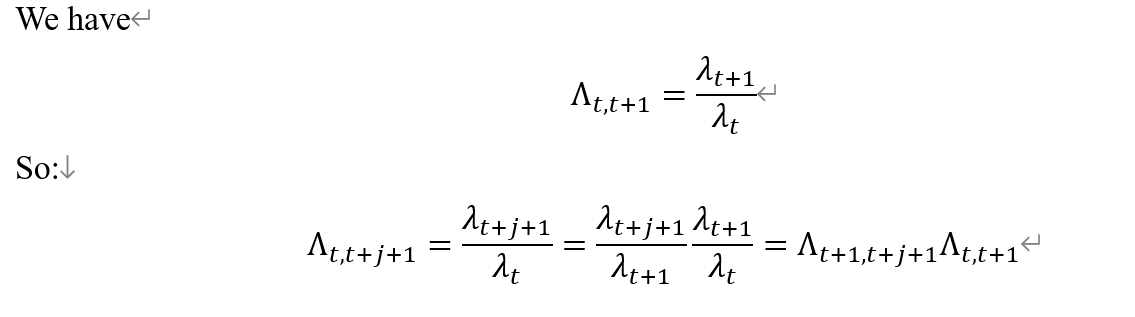Gertler & Karadi (2011) First order conditions

[Robert]

Hi everyone,

This is a quick questions for all those who have replicated or worked with the Gertler & Karadi (2011) unconventional monetary policy model.

I am currently trying to understand the code which in turn means making sense of the FOCs. At the moment I am having to trouble to understand where the two equations under condition (11) come from:

\nu_t = E_t \Big[ (1-\theta) \beta \Lambda_{t,t+1} (R_{k,t+1} - R_{t+1}) + \beta \theta x_{t,t+1} \Lambda_{t,t+1} \nu_{t+1} \Big]

and

\eta_t = E_t \Big[ (1-\theta) + \beta \Lambda_{t,t+1} \theta z_{t,t+1} \eta_{t+1} \Big]

In the paper it says: “The variable \nu_t has the interpretation of the expected discounted marginal gain to the banker of expanding assets Q_t S_{j,t} by a unit, holding net worth N_{j,t} constant, and while \eta_t is the expected discounted value of having another unit of N_{j,t}, holding S_{j,t} constant.” The discounted lifetime net worth of the banker is expressed as:

V_{j,t} = \max E_t \sum_{i = 0}^{\infty} (1-\theta) \theta^i \beta^{i+1} \Lambda_{t,t+1+i} \Big[ (R_{k,t+1+i} - R_{t+1+i}) Q_{t+i} S_{j,t+i} + R_{t+1+i} N_{j,t+i} \Big]

I was therefore thinking this expression above just gets maximised w.r.t. to Q_t S_{j,t} and N_{j,t}, but it turns out this is not the case (or I am wrong). Any help would be greatly appreciated where condition (11) in the paper comes from. Many thanks!

Rob

[jpfeifer]

It looks as if that is simply a way of writing V_{j,t} recursively by splitting up the terms.

[Bandel]

[Robert]

Many thanks @jpfeifer and @Bandel for both of your help! I will it give it a go now.
Rob

[Robert]

Thanks @Bandel for your derivations, I just went through them and they make sense. Just a quick question regarding:

\small V_{t} = \nu_t Q_t S_{t} + \eta_t N_{t} = \underbrace{ (1-\theta) \beta \Lambda_{t,t+1} \Big[ (R_{k,t+1} - R_{t+1}) Q_{t} S_{t} + R_{t+1} N_{t} \Big] }_{ \text{first term} = V_{j,t}} + \underbrace{ \beta \theta \Lambda_{t,t+1} (\nu_{t+1} Q_{t+1} S_{t+1} + \eta_{t+1} N_{t+1} ) }_{ \text{second term}}

I understand where the first term comes from, which is simply the discounted net worth of bankers, as shown in my original post. The second term is that the recursive part, i.e. V_{t+1} as pointed out by @jpfeifer? Thanks!

[Bandel]

Yes that is the recursive part as @jpfeifer pointed out.

[Robert]

Thanks @Bandel! I understand how you get from the first to the second line. Could you please explain you can expand \Lambda_{t,t+j+1} to find \Lambda_{t,t+1} \Lambda_{t+1,t+j+1} (i.e. going from the second to the third line)? Many thanks

[Bandel]

[Robert]

Thanks @Bandel, I had a feeling that opening up \Lambda_{t,t+1} could be another way to get your result - turns out it is. Let me have a look and get back to you. Thanks already for all your help!

[Robert]

Hi @Bandel, can I just double check with you please how you get from the third to the final line, where you find the sum is equal to V_{t+1}. In the third line you change the sum starting value back to 0 and \Lambda_{t+1, t+1+i} becomes \Lambda_{t+1,t+i} and N_{j,t+1+i} becomes N_{j,t+i} (my notation is slightly different than yours). So we find that:

V_{j,t} = (1-\theta) \beta \Lambda_{t,t+1} N_{j,t+1} + \theta \beta \Lambda_{t,t+1} \underbrace{ \sum_{i = 0}^{\infty} (1-\theta) \theta^{i-1} \beta^{i} \Lambda_{t+1,t+i} N_{j,t+i} }_{V_{j,t+1}?}

How do you know that this sum is equal to V_{j,t+1} and not V_{j,t-1}. I plugged values in and I actually reach the conclusion that I’ve obtained the latter. This should hopefully be the last question I have, thanks!

[Bandel]

You can get this by comparing the change of the superscript of Vt