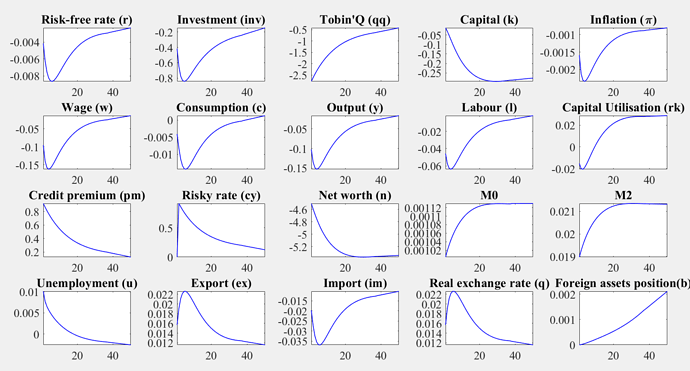
Hi Professor,
How could I modify the code below to that Matlab could show the 1 unit standard error bands for my each of my IRF subplots?
The data file I am uploading is IRFfull.csv
the code I am using is:
clear all; close all; clc;
load IRFfull.csv;
varname=char('Risk-free rate (r)','Investment (inv)','Tobin''Q (qq) ',...
'Capital (k)','Inflation (\pi)','Wage (w)','Consumption (c)',...
'Output (y)','Labour (l)','Capital Utilisation (rk)',...
'Credit premium (pm)','Risky rate (cy)','Net worth (n)',...
'M0','M2','Unemployment (u)','Export (ex)','Import (im)',...
'Real exchange rate (q)','Foreign assets position(b)');
for i=1:20
subplot(4,5,i)
plot(IRFfull(:,i),'b','LineWidth',1);
axis tight;
ax = gca;
ax.YAxis.Exponent=0;
title(deblank(varname(i,:)));
set(gca,'FontSize',16, 'FontName','Times');
end;
which gave me the plot as below:
I wanted to add the error band (1unit standard deviation) as :
shadedErrorBar.m (5.1 KB) demo_shadedErrorBar.m (1.9 KB)
IRFfull.csv (11.6 KB)
The shaded error bar M files are attached…