Dear Dynare team,
I working on a paper where I need to find optimal monetary policy rule parameters based on comparing household welfares. Suppose, we have a standard Taylor rule
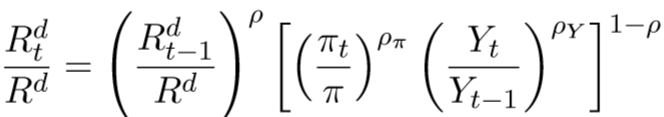
As I understand, we need to create a 3 dimensional grid in this case, and then search for the optimal values for \rho, \rho_\pi, and \rho_Y over this grid by comparing welfares in each grid point?
Suppose, I choose for the intervals: [0,1] for \rho, [1.1,6] for \rho_\phi, [0,3] for \rho_Y. If I assume the grid step for each parameter is 0.1, then we have (1/0.1) ((6-1.1)/0.1) (3/0.1)=14700 points. Does not this take a long time to solve in Dynare? Is there a code for this exercise? If yes, could you please send it to me, if it is possible?
If, for example, using an optimizer is possible, what kind of optimizer I can use? How can I integrate this optimizer in my Dynare code? Is there a sample code for such type of exercise?
Sincerely,
Archil