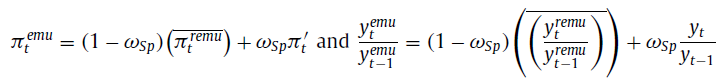Dear All,
I’m new to using Dynare. I’m trying to replicate the Taylor rule of the paper “Financial and fiscal shocks in the great recession and recovery of the Spanish economy”, however I have problems on dealing with the following equations:
(GDP_euro_area/GDP_euro_area(-1))=(1-omega)x(GDP_remu/GDP_remu(-1))-omega x(GDP/GDP(-1)) and
pi_euro_area=(1-omega)x pi_remu+omega x pi
since the ratio (GDP_remu/GDP_remu(-1)) and pi_euro_area are defined as exogenous.
How do I account for these variables in Dynare?
Thanks in advance for help!
Hi, framarz.
You will have to provide more details and be specific regarding your question so that we can help you.
-
What do you mean by “account for these variables” in dynare?
-
Attach the paper you are trying to replicate and any .mod file you have, even if it is incomplete.
-
Are you sure inflation and GDP ratio are exogenous? This sounds weird, since you have a Taylor rule.
It depends on what you are trying to do. What did the original paper do? My guess is specify an exogenous process for those two variables, e.g. a VAR.
Thank Tavinho and jpfeifer for answer,
I want try to model a Taylor rule for a small open economy that belongs to a monetary union such as the euro area. To do this, I am following the paper I have attached here.
The taylor rule is at pag 12.
My problem is that in this paper is only written that ratio y_remu/y_remu(-1) and pi_remu are exogenous but it doesn’t provide any exogenous process and I don’t know how to continue to implement this Taylor rule.
Thank you in advance for helping me
1-s2.0-S001429212030101X-main.pdf (2.9 MB)
The paper does not say these variables are exogenous. What it actually says is that the steady state level of these variables are exogenously determined.
Take a look at the definitions right below the taylor rule:
where \overline{\pi_t^{remu}} and \overline{\frac{y_t^{remu}}{y_{t-1}^{remu}}} are parameters that pin down the steady state of \pi_t^{emu} and \frac{y_t^{emu}}{y_{t-1}^{emu}}, respectively. But \pi_t^{emu} and \frac{y_t^{emu}}{y_{t-1}^{emu}} are endogenous objects! They depend on \pi'_t and y_t.
Hope this helps.
Thank you for the answer,
I tried to implement this taylor rule,the code works, however Model_Diagnostics gives me a problem of colinearity between the equation of the ratio GDP_emu/GDP_emu(-1):
(GDP_emu/GDP_emu(-1)(=(1-omega_sp)(y_remu/y_remu(-1))+omega_sp(GDP/GDP(-1))
and the exogenous AR(1) process for y_remu/y_remu(-1):
log(y_remu)-log(y_remu(-1))=para-rho_GDP_remu*(log(y_remu(-1)-log(y_remu(-2)))+epsilon_GDP_remu
I think the problem is related to the fact that GDP_emu is used only to determine the growth rate of GDP in the Eurozone but there is no equation in the model to determine it.
Could you suggest me a way to solve this issue,please?
Thank you in advance
Please provide your codes. Maybe someone will have time to walk through it and find the answer.