Dear Professor Pfeifer,
I hope you are doing well. I do have a question regarding the measurement equations used during the estimation process. I know that measurement equations are for matching the data with a model. However, I am confused by the use of exogenous variables in the measurement equations.
For example: dyt = y(t)-y(t-1)+trend, for output growth (in Smets and Wouters (2007) and many papers). I understand this equation.
Another example: dyt= y(t)-y(t-1)+z(t)+ctrend (in FRBNY DSGE model paper by Del Negro et al (2013). I got confused here. I get entirely different time-series of smoothed output (y_t) when I use the productivity term in the measurement equation.
My concern is that while making a model economy, we believe that there are different types of shocks affecting the economic variables. However, the second type of measurement equation says that output growth is primarily driven by productivity shock only. Is the assumption in the measurement equation not in contrast with the model? Or am I wrong in understanding the measurement equation?
I wonder if you could help me understand this issue?
Sincerely,
Niraj
I am not sure what you mean. If you have z(t) in there, you assume that there are shocks to the trend growth rate.
Of course, detrended output y(t) will look different in this case.
Thank you, professor for you your reply!
Niraj
Hello, professor!
I am sorry for asking many questions to you nowadays. But, I want to utilize this summer to learn the estimation process. As only one or two people in my department work in DSGE model and they also do not do estimation. Therefore, Dynare forum has been very important source of knowledge for me in regards to estimation. Thank you once again for answering my questions quickly.
Let me get back to our discussion about the measurement equation. I have estimated the Smets and Wouters (2007) model with their measurement equation and then later I added some exogenous processes in those equations.
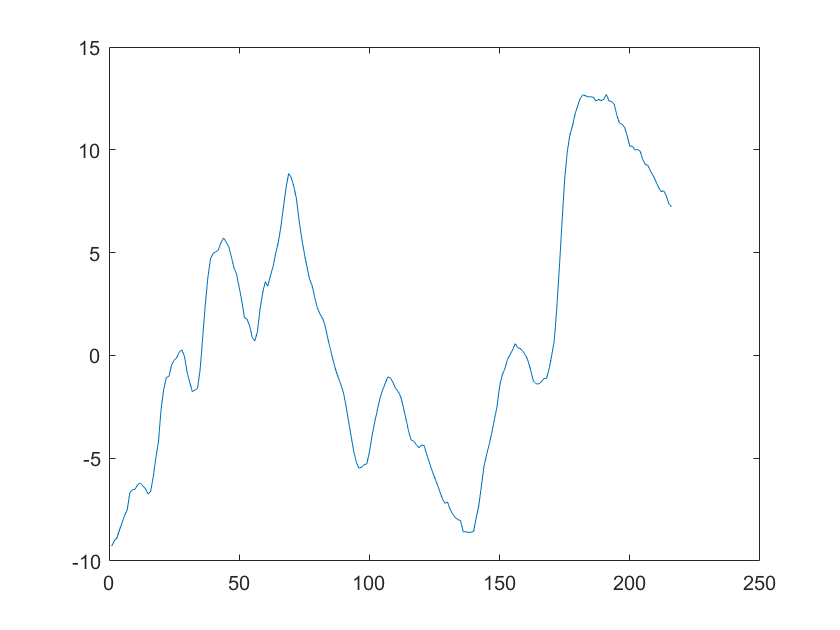
I have attached the time series of smoothed output (y_t) obtained under both conditions. The first image shows smoothed GDP when the measurement equation does have an exogenous process. While second image shows the time-series of output when the measurement equation does not contain any AR(1) process.
Is it that the measurement equation with exogenous variables gives the business cycle component (cyclical component ) of variables? I am confused as a cyclical component would have different values than the trend, which is not in my case. Could you write me what I am missing here to understand this thing?
I used the following measurement equations for obtaining the first graph:
dy= y-y(-1)+ a+ trend; (productivity shock for output equation)
labobs = lab + constelab; (Labor supply)
LS= lab + w-y+ Lstar; Labor share
pinfobs = 1*(pinf) + constepinf; (Inflation)
robs = 1*(r) + conster; (Interest rates)
Thank you once again for your answer and time.
Sincerely,
Niraj
What constitutes the cyclical component depends on your definition of it. In the data, you observed trending output. You now decompose this into
- A linear trend plus a cyclical component (here the decomposition is clear-cut)
- A linear trend, a “cyclical” component, and a growth rate shock
a, which explains why y now takes on a different meaning. In a model with shocks like that, people usually consider the growth rate of output to measure cyclical fluctuations.
The growth rate shock a usually also captures some cyclical element.
Thank you , Professor for your answer. I am now clear in this issue.