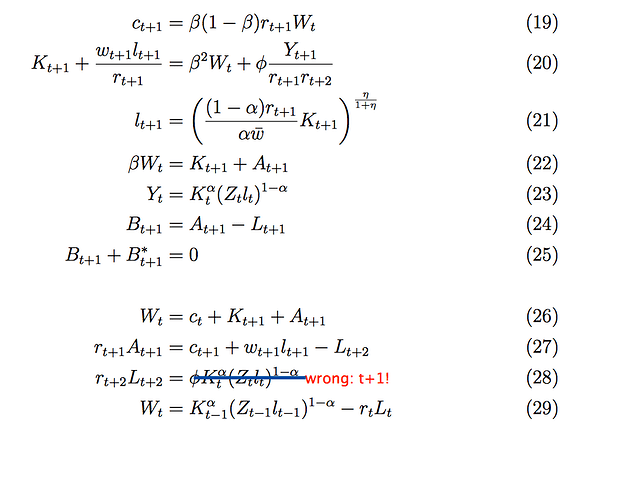Dear Prof. Pfeifer
I’m trying to replicate the following two-country dynamic general equilibrium model, but get actually the error “Blanchard Kahn conditions are not
satisfied: indeterminacy”. I think that my timing structure is wrong. But I think that net demand for bonds B, capital K, the amount of borrowings L and bond holdings A are predetermined variables(?)
I marked the corresponding explanations in the paper with a green square and would be extremely happy for any kind of help. I attached the mod-File and the formulas I’m using.
I also added a presentation from the authors concerning the paper.
Edit: I also simplified the whole thing to a problem with just one country and added this file.
Thanks a lot and Best regards
00_Slides.pdf (205.0 KB)
bbOneCountry.mod (2.9 KB)
bbKopie2.mod (3.6 KB)
00_Paper 01.pdf (749.1 KB)
The guiding principle in Dynare is to enter the FOCs from the perspective of decisions taken at time t. The attached paper often refers to decisions taken in the future, e.g. t+2. But you need to enter them from the perspective of time t. That relates to e.g. equation (19) .
I see the point. So as production is determined in t+1 as Y = K^α(Zl)^(α-1) I can write it for period t as Y(-1) = K(-1)^α(Z(-1)l(-1))^(α-1)?
No, using the stock at the end of period notation to make clear what is predetermined, you would have
Y_t=K_{t-1}^\alpha(Z_tl_t)^{\alpha-1}
because labor and therefore output are only decided upon after Z has materialized. In contrast, capital has been chosen before Z realized.
Okay. I still don‘t get it totally, sorry. Can you give me an example for equation (19), the consumptiom at t+1? How I would have to put this one into dynare with the right timing now?
You need to determine consumption at time t. So you have to use
c_t=\beta(1-\beta)r_t W_{t-1}
Okay, then I think I got it right. So I have to rewrite all equations to apply for time t and then again predetermine capital, borrowings and bonds. So e.g. instead of Y(t+1) = K(t+1)^α(Z(+1)l(+1))^(1-α) I have to use Y = K(-1)^α(Zl)^(1-α) as written above.
My model is now running, I don’t get the indeterminacy error anymore. Can I therefore assume that I got the timing of my variables right or could there be other working specifications and mine is still wrong?