Hello Dr.Feifer,
I am running an NK model of household heterogeneity in which I also introduce human capital as ha, hb, and H in the mod file, where ha and hb are the human capital of two different households.
And H is the sum of ha and hb.
I refer to the setting of physical capital Ka (Ka(+1)=(1-deltak)Ka+deltahIak;) for human capital ha and hb, i.e. ha(+1)=(1-deltah)ha+deltahIah;
where ha is equivalent to Ka as a stock and Iah is equivalent to Iak as a flow. But I have encountered the problem in the solution process as shown below, I hope you can help me!
model1.mod (9.8 KB)
Hi chenxin,
your model_diagnostics; command shows you where the problems are:
Warning: Some of the parameters have no value (b2, b3) when using model_diagnostics. If these parameters are not initialized in a steadystate
file or a steady_state_model-block, Dynare may not be able to solve the model. Note that simul, perfect_foresight_setup, and
perfect_foresight_solver do not automatically call the steady state file.
MODEL_DIAGNOSTICS: The Jacobian of the static model is singular
MODEL_DIAGNOSTICS: there is 1 colinear relationships between the variables and the equations
Colinear variables:
Ca
La
Na
ea
ha
qa
Ka
Ba
wa
Iah
Iak
Oa
Cb
Lb
Nb
eb
hb
qb
wb
Ibh
Ob
xi
R
tau
RK
pi
C
L
H
Ik
N
K
B
e
q
Ih
W
KG
Y
G
IG
AIG
AUX_ENDO_LAG_44_1
Colinear equations
18 19 20 21 23
MODEL_DIAGNOSTICS: The presence of a singularity problem typically indicates that there is one
MODEL_DIAGNOSTICS: redundant equation entered in the model block, while another non-redundant equation
MODEL_DIAGNOSTICS: is missing. The problem often derives from Walras Law.
I suggest starting with these issues.
Yes, I used model_diagnostics to check that the model also had covariance problems, but I was doing a TANK model that heterogeneized the families, and there were some set-up similarities between the two families. How can I deal with the covariance problem in this case? I have just modified the problem for b2 b3 and the modified code is as follows.
model1.mod (9.8 KB)
I do not know your model, so it is impossible for me to judge what equations could be the cause of the colinearity issue. But I think that there might also be a timing error, which usually is the reason for problems. You stated that the variable ha also is a predetermined variable, as capital, but in at least one equation - I did not check all - Ca=wa+ha+Oa-tau_bar*tau;. I am not sure if this is on purpose but I would think that consumption depends on the capital available, which should than be ha(-1).
Since it is a big model, and probably you started from some working code, I suggest going back to it and adding additional sectors one by one. This way you can be sure that it works.
Check your timing and simplify the model
Ka(+1)=(1-deltak)*Ka+deltak*Iak;
looks wrong.
Hello dear professor.
I am following the advice and making a simple RBC model, but after running the code I get the error "Blanchard & Kahn conditions are not satisfied: indeterminacy.
logonlylita1.mod (3.1 KB)
Your timing with respect to stock variables looks inconsistent.
I solved this problem and ran the steady state, but also got the error “Blanchard & Kahn conditions are not satisfied: no stable equilibrium.” when doing Bayesian estimation
bayesian.mod (8.5 KB)
My data is here
model_data.mat (2.9 KB)
See
And professor, does this have anything to do with the non-zero residuals of Equation 12 in my model, and how do I solve the problem that the residuals of Equation 12 are not zero?
The equation
wb+qb-Cb-xi_bar*xi=gamma*cbxi_bar*Nbs-ebs*cbxi_bar*(eb-Ob);
seems to be incorrectly linearized, because
gamma*cbxi_bar*Nbs
is a constant.
Dear Professor, I was debugging the code and once again I got the error “One of the eigenvalues is close to 0/0 (the absolute value of numerator and
denominator is smaller than 0.0000!”). You told me before that there is a problem with timing, but I’m not sure what principles I need to follow to debug the timing problem, can you provide me with some learning materials to solve the timing problem?
Here is my latest code
tiaoshi.mod (6.7 KB)
And professor, my equation shows the existence of covariance in the vendor sector, and my vendor sector is a relatively standard producer of final and intermediate goods. Why is there a covariance here? Here I changed the manufacturer’s sector to the standard one and it still shows “One of the eigenvalues is close to 0/0 (the absolute value of numerator and denominator is smaller than 0.0000!
denominator is smaller than 0.0000!” error, with "model_diagnostics;
"After checking, it still shows that there is multicollinearity in the equations of the vendor’s department. I don’t know how to solve this problem. Can you help me?
addwage.mod (6.8 KB)
For now, focus on the timing issue. It is most probably related to the sectoral structure. See
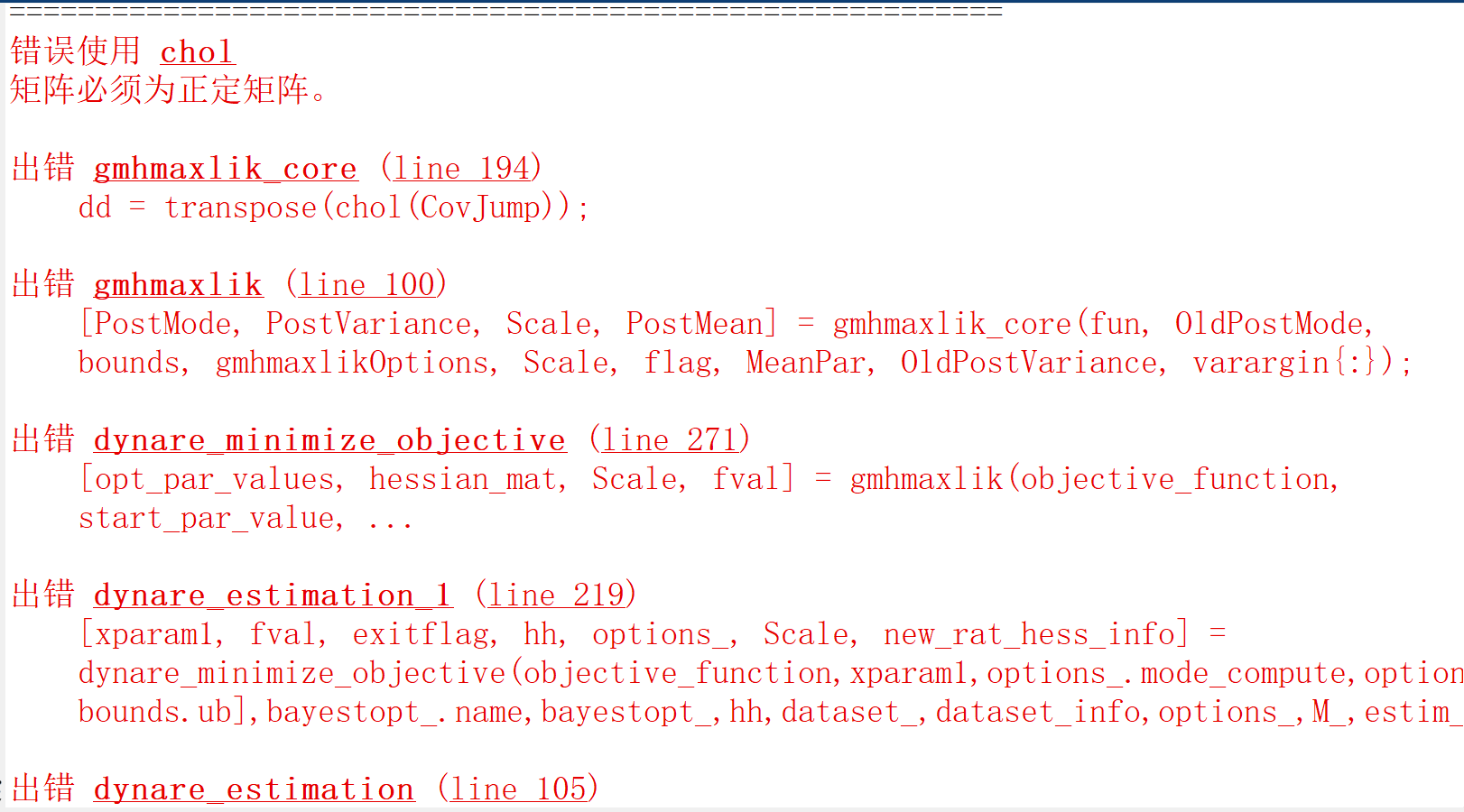
Dear Professor I made an impulse response plot with the information you gave me, but I still get an error when doing Bayesian estimation.
bayesian.mod (8.5 KB)
What is the problem you are experiencing? And why is your pi_obs still trending?
Is the reason for the above error because of the trending of pi_obs?
Which error are you getting?