Theoretically, it seems the effect of terms of trade shock on export is ambiguous, depending on the way one builds the model. How to know which one to choose when building a DSGE model? Should you build a VAR model first to guide your choice?
In (Computational Macroeconomics for the Open Economy G. C. Lim and Paul D. McNelis - chapter 7), TOT affects export negatively because there is a fall in the relative price of home goods, which encourages consumers to shift to home goods. The terms-of-trade shock discourages export. The production sectors are export and home production sectors.
In (Open Economy Macroeconomics, M. Uribe, and S. Schmitt-Groh´e - Chapter 7), there is a substitution in production away from importable goods and toward exportable goods after a TOT shock. The production sectors are import and export production sectors.
By the way, is the effect also ambiguous on total output? My instinct says yes. I mean it depends on how much is gained and how much is lost, right?
I am not familiar with those models, but I can imagine that effects depend on the strength of income vs. substitution effects. For modeling there are usually two ways out:
- You use a VAR to find out which way the variable is supposed to go and the adjust the model in that direction.
- You have micro estimates of the required elasticities that will tell you which effect is supposed to dominate.
1 Like
Hi prof. Pfeifer, many thanks for your reply. I have some idea. Your comment will be much appreciated.
- Use several specifications of the VAR model to fit your data.
- If results are similar, then great!!. Adjust your DSGE model accordingly.
- If different VAR specifications give different results. Then adjust your DSGE model for each result. And use the model evaluation criteria in dynare to select the best model. Thus, assuming you are estimating your DSGE model.
I don’t know how 3 would work. There will be only one parameter estimate, i.e. the one that fits the data best. So it would only be feasible if the different results are not a matter of parameter values but fundamental model structure.
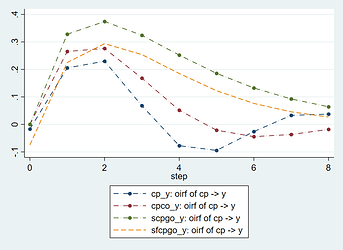
Yes, on number 3, I meant different models with different fundamental structures. For example in the plot below, I consider 2-variable VAR, 3-variable VAR, 3-variable SVAR, and FAVAR models. Pretty much similarly in the first plot, I would say.
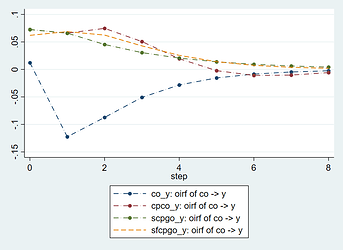
But suppose, for example, that the IRFs were significantly different (second plot), then I may want to do what I said in number 3 in the previous post. This is just an example though, and here, I could ignore the one IRF that is significantly different (via some sort of majority voting). But in case two of them had similar shapes and the remaining two also had similar shapes. Then it is kinda difficult to choose which one is more correct. Or probably, a third model…
effect of cocoa price shocks on real GDP per capita
effect of cocoa output shocks on real GDP per capita