Disinflation model

Perfect foresight simulations
1

Hello all,

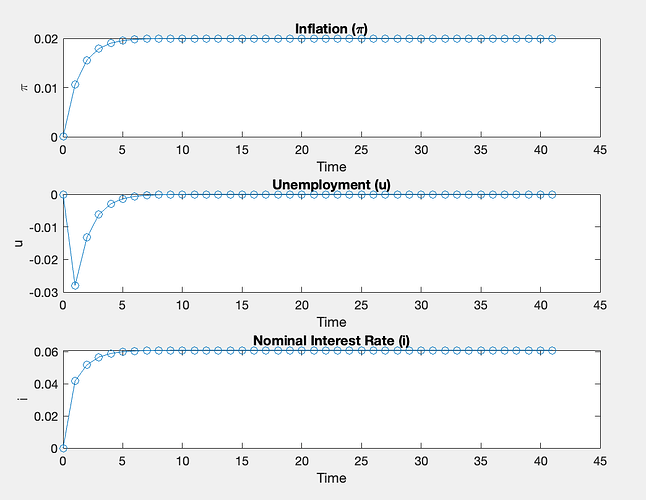
So, it’s been some days working on this but I don’t seem to get things right. I am completely new to Dynare. I am trying to solve a disinflation path numerically. I have tried to solve it as a stochastic simulation and now I am trying to do it as a foresight simulation. I have tried to set different initial values, tried to change the model… but still, my model seems off. I get initial inflation of zero that is stabilised then at 0.02. Unemployment starts at zero and then goes negative. I have also i starting at zero and stabilising itself at 0.06. I just think I might be telling the program the wrong initial values. Changing them (or even deleting u and i) doesn’t change anything. Any chance anyone know how to help?

Thanks in advance!

% 1. Declare the endogenous variables:
var pi u i;

% 2. Declare and set the parameters:
parameters beta pi_bar lambda xi kappa rho;

beta   = 0.96;          
pi_bar = 0.02;         
lambda = 0.75;          
xi     = 0.2;             ´
kappa  = 10;              
rho    = -log(beta);      

% 3. Model Equations:
model;
    % (i) Phillips Curve:
    pi = lambda * pi(-1) + (1 - lambda)*pi_bar - xi * u;
    
    % (ii) Target Rule
    1 - exp(-u) = xi*kappa*(pi - pi_bar) + lambda*beta*(1 - exp(-u(+1)));
    
    % (iii) Euler Equation:
    i - u = rho + pi(+1) - u(+1);
end;

% 4. Initial values:
initval;
    % For a perfect foresight simulation these are our “guess” values for period 0.
    pi = 0.05;         % We set the time-0 value at the steady state (2%)
    u  = 0;
    i = rho + 0.05;
end;

% 5. Historical values:
histval;
    % Here, we force Dynare to “see” that prior to period 0, inflation was 5%.
    pi(-1) = 0.05;
end;

% 6. Steady State Calculations:
steady_state_model;
    u  = 0;
    pi = pi_bar;
    i  = rho + pi_bar;
end;

steady;
resid;

% 7. Perfect Foresight Simulation:
perfect_foresight_setup(periods = 40);
perfect_foresight_solver;

% 8. Plot the Simulation Results:
T = 0:(size(oo_.endo_simul,2)-1);

figure;
subplot(3,1,1);
plot(T, oo_.endo_simul(1,:)','-o');
title('Inflation (\pi)');
xlabel('Time');
ylabel('\pi');

subplot(3,1,2);
plot(T, oo_.endo_simul(2,:)','-o');
title('Unemployment (u)');
xlabel('Time');
ylabel('u');

subplot(3,1,3);
plot(T, oo_.endo_simul(3,:)','-o');
title('Nominal Interest Rate (i)');
xlabel('Time');
ylabel('i');

```
2

What exactly is the problem? The simulation correctly converges to the steady state.

3

The issue seems to be the initial values. Inflation starts at zero, unemployment goes negative… I don’t see a disinflation path in that sense.

Screenshot 2025-04-15 at 12.13.46
Screenshot 2025-04-15 at 12.13.461044×808 29.7 KB

4

Then you need to understand the working of the model. Past inflation is the only state variable in your model. It starts from below steady state. Unemployment endogenously adjusts according to the equations you specified.

5

Thanks for your help :slight_smile: It is just that I do not understand why, even if I just put pi as initval then the model behaves the same…
initval;
pi = 0.05;
end;

I might be missing something about histval or initval… but after many trials, I cannot figure out what it is.

6

Now I got it. The histval-block was wrong. Use
disinflation.mod (1.6 KB)

7

Thank you so so much. I got now to get the model working with the right results.