Deterministic shock and rank conditions

Perfect foresight simulations
1

Hello,

Please see file attached
Gali5.mod (560 Bytes)

The purpose of this script is to consider a given negative shock (rho) to a very simple model, which brings about a fall in the interest rate and output gap. When defining the interest rate using 18) one obtains a convergent solution and the indication that the rank condition is verified. However when using specification 19), it appears the message “rank condition is not satisfied”, though the results wrt the variables appear to be “consistent”.

Generally, I also found out that using more elaborate models subject to a deterministic shock, the vectors obtained contain n+2 elements, n being the number of simulations specified. The first element is 0 (it is a linear model), as well as the last element. The former seems to reflect the s.s. initial values, but the latter buffles me.

Regards,
Jose

2
  1. What do you mean with specification 19?
  2. Please consult the Dynare manual on perfect foresight simulations. You always need initial and terminal conditions. Those explain the two additional periods.
  3. Your model is not linear. As Dynare says

WARNING: you have declared your model ‘linear’ but you are using a function (max, min, abs, sign) or an operator (<, >, <=, >=, ==, !=) which potentially makes it non-linear.

  1. Solving models with an occasionally binding constraint is tricky, because the Jacobian will be singular.This may require special solvers. Please consult DSGE_mod/Gali_2015 at master · JohannesPfeifer/DSGE_mod · GitHub for replication files for Gali’s book.
3

Dear Johannes Pfeifer,

1- Specification 19) in the script sent to you reads: "id = max (log(1), rho). When using it instead of 18) while the variables obtained appear to be “consistent”, one is confronted with the message that rank conditions are not satisfied. This does not occur when line 18) is used.

2- Noted, thank you.

3- When running Dynare (4.4.3) no such warning was produced and the model was declared linear as you know.

4- Thank you for sharing the scripts. They are far more elaborate when considering my limited knowledge of Dynare. For the record, I copied and pasted your script "Gali_2015_Chapter5_Commitment_ZLB. When running it, Dynare generated two error messages:
Error: File: Gali5C.m Line: 159 Column: 32
The expression to the left of the equals sign is not a valid target for an assignment.

Error in dynare (line 180)
evalin(‘base’,fname) ;

5- The question remains: The results yielded by Dynare using the very simple example are acceptable even when using line 19 instead of 18?

Thank you,
Jose

4
  1. It is not surprising that this specification does not work, because it involves a constant interest rate. Without a proper interest rate rule, you will not get a unique determinate equilibrium.
  2. Please use Dynare 4.5 not 4.4 for the Gali_2015_Chapter5_Commitment_ZLB.mod-file
5

Gali5.mod (1.1 KB)

Dear Johannes Pfeifer,

1- Evidence suggests that in spite of the Dynare message, the simple script appears to work. I have attached it incorporating your graph generating codes. Please, run the script using both specifications (lines 18 or 19); recall that under the former hypothesis the rank condition is satisfied. You may have to use version 4.4.3.

2- I have also attached the graphs obtained under both scenarios containing output gap (x), inflation (pip), and the nominal interest rate (id). I was not able to get a graph using Dynare for the natural interest rate (rho); how can I do it? It is apparent that under 19), one replicates Gali’s figure 5.3 under discretion.

3- The initial value for id is zero. The default terminal value is also zero. My intention is simply drop the last value or keep it at one (not annualized) as in the Gali’s picture. How do I do it?

4- As a curiosity I ran your script for the Gali_2015_Chapter5_Commitment_ZLB using 4.4.3 simply replacing the two “perfect foresight” codes with “simul”. The program ran normally. However both inflation and the output gap are pinned down to zero, while the natural interest rate exhibits the same pattern as in Gali 2015.

5- The question raised in my previous mail (also nº5)

Thank you,
Jose

6

Dear Johannes Pfeifer,

I could not upload the second set of graphs, thus I am sending another “reply”.

Best,
Jose

7
  1. The case you have is indeterminacy, i.e. there is no unique solution. It is no wonder you get a solution, but it may not the only one. That being said, it could be that your terminal condition may actually be pinning down one unique solution (which is usually what the second unstable root does)
  2. You defined rho as an exogenous variable. Thus, you are looking in the wrong spot. The correct code would be
figure

subplot(2,2,1)

plot(0:options_.periods,oo_.endo_simul(strmatch('x',M_.endo_names,'exact'),M_.maximum_lag+1:M_.maximum_lag+1+options_.periods),'-x')

axis([0 9 -15 5])

subplot(2,2,2)

plot(0:options_.periods,oo_.endo_simul(strmatch('pip',M_.endo_names,'exact'),M_.maximum_lag+1:M_.maximum_lag+1+options_.periods),'-x')

axis([0 9 -5 5])

subplot(2,2,3)

plot(0:options_.periods,oo_.endo_simul(strmatch('id',M_.endo_names,'exact'),M_.maximum_lag+1:M_.maximum_lag+1+options_.periods),'-x')

axis([0 9 -1 2])

subplot(2,2,4)

plot(0:options_.periods,oo_.exo_simul(M_.maximum_lag+1:M_.maximum_lag+1+options_.periods,strmatch('rho',M_.exo_names,'exact')),'-')

axis([0 12 -6 6])

  1. You should be able to use initval and endval. See the manual.

  2. Sorry, but I don’t have the time to trace out what is going on in the old version. There were a couple of bugs that have been fixed in Dynare 4.5, which is the reason you should use that version.

  3. That depends on the answer to 1). My hunch is that the terminal value selects a unique equilibrium and you should be fine using 19

8

Dear Johannes Pfeifer,

Thank you for your time and insights.

With respect to 5 above, I developed a more complete script encompassing areas of my research and was confronted with similar warnings, but apparently consistent outcomes, when using specifications as in 19 and 18. It would appear that your “hunch” may be grounded, even though no terminal value is specified.

Best,
Jose

9

The point is that the Blanchard-Kahn conditions refer to a system of linear difference equations. The conditions need to be satisfied in order to have a unique stable solution. To have that, we need a stable root for every state variable as otherwise the system would explode. At the same time, we need an unstable root for every forward-looking variable in order to rule out indeterminacy.
The nonlinear model you consider is different in the respect that i) it is nonlinear and therefore not governed by the same rules as linear systems and ii) there are explicit terminal conditions restricting the path of forward-looking variables. That is why my hunch was that the “indeterminacy” case you are getting may not be problematic.

10

Thank you, Johannes Pfeifer.

11

Dear Johannes Pfeifer,

Is it possible to download the most recent Dynare version (4,5) while maintaining operational in the same computer a previous version (4.4.3)?

Thank you,
Jose

12

Sure. Remove all paths to Dynare in Matlab and then for every session just add the path to the matlab-subfolder of the version you want to use.

13

Dear Johannes Pfeifer,

Please bear with me. If I understood you correctly I should use the following commands in Matlab, after downloading Dynare 4.5.1 :

rmpath c:\dynare\4.4.3\matlab
addpath c:\dynare\4.5.1\matlab

Should I want to revert to the older version, simply reintroduce the same commands switching the version numbers.

Thank you,
Jose

14

The way I work is not to have any path to Dynare in the Matlab startup paths. I then use

addpath c:\dynare\4.5.1\matlab

or

addpath c:\dynare\4.4.3\matlab

depending on which version I need. But I don’t see a reason why end-users should still work with 4.4.3.

15

MFDF.mod (2.8 KB)
Dear Johannes Pfeifer,

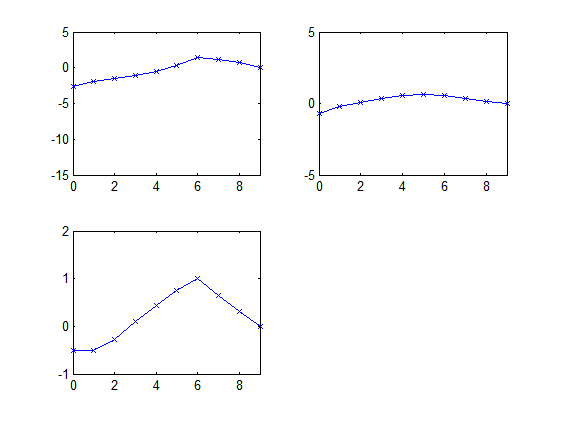
Following the previous correspondence, where figure 5.3 (Gali 2015) is contemplated, I added a few more specifications to a still simple model. Please see the attachment.

The idea is to consider scenarios whereby policy authorities decide to increase spending or cut taxes, after an unexpected negative shock to the natural rate (rn) conducive to a drop in output and a ZLB liquidity trap.

I would like to raise the following questions:

1- When considering three “varexos” within this attachment, Dynare (4.5.1) works fine. When adding a fourth “varexo”, Dynare delivered invariably an error message as detailed in the script (lines 22-24).

2- The number of simulation periods translates into different values of the variables, even though one obtains the message “perfect foresight solution found”. Should some criterion be followed?

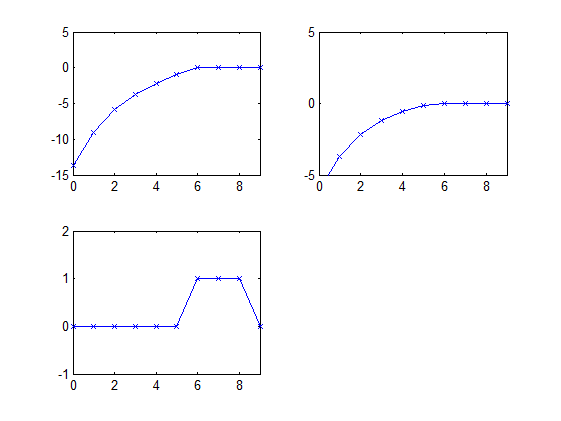
3- When considering a debt financed stimulus, using line 55, the results appear to be consistent and the ZLB liquidity trap “respected”, However, when specifying a money financing process using instead line 56, nominal interest rates are (generally) positive. The question thus, is how to incorporate the ZLB liquidity trap in this financing regime?
When you wrote the codes to replicate Gali’s figure 5.3 (2015) under commitment, there is an improvement to the hypothesis obtained under debt financing without commitment, as defined in line 55. My interpretation is that these codes proxy the relevance of forward guidance. Does this mean that if one wants the incorporate the ZLB liquidity trap one has its options restricted? I tried to use your codes (please see lines 58-60), but to no avail. Any suggestions and help, if possible, would be appreciated?

4-Is it possible to overlay graphs using Dynare, say to compare the results under a tax cut or a boost in government spending? An hypothesis is to rely upon Matlab (more user friendly for this purpose), but then the number of periods is at stake as well as the initial and terminal values.

Best regards,
Jose

16

Dear Johannes Pfeifer,

Please disregard question 1. After reinitiating the computer, Dynare worked fine (?).

Regards,
Jose