Deterministic model with a shock to a parameter

[kofiemma]

Hi, I am reading this book and the authors calibrate a shock to a parameter A (which shows up in the export equation below). Their model is deterministic and they simulate the effect of a shock to the parameter A. They mention they used Dynare.

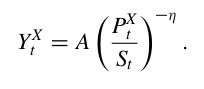
I do not have their code but I guess they will declare A as a variable in their mod file, right? Not as a parameter. If so, does using A_t \sim AR(1) instead of A in the above equation change anything? Thanks!

Or perhaps there is a way to calibrate a shock to a parameter in dynare?

[jpfeifer]

In perfect foresight, you would simply specify A to be a varexo.

[E.Ahmed]

It means that
A_t = A + \epsilon_t ,
with \epsilon_t = \rho * \epsilon _{t-1} + \eta_t and \eta \sim iid ~normal (0, \sigma ^2)
If there is a perfect foresight like noted by jpfeifer, then A_t = A + E(\epsilon) = A