Dear all,
I am struggling to understand the Measurement equations part of the Bayesian estimation process. I use a TANK model, the one from the paper of Bilbiie (2013). I have three log-linearized equations. The three following equations represent the measurement equations of the model :
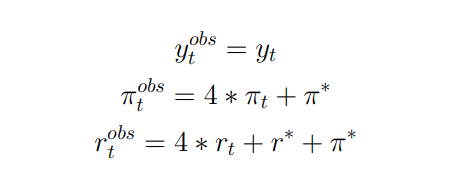
I am not fully sure about how to transform the data. In the paper above, it seems that the following data are considered : the cycle component of log real gdp per capita ( multiplied by 100), inflation is annualized percentage change of CPI, and interest rate is the annualized rate in percent. Is it correct ? Should not we use the log form of interest rate and inflation instead ? Why do we put the steady state value of both inflation and interest rate in the third equation ?
Thank you for your help !
Simulation.m (1.8 KB)
Which exact paper are you referring to? The means in the last two equations are there because the empirical data was most probably not demeaned.
Thank you professor, for your answer. I am refering to the paper : Asset Market Participation, Monetary Policy Rules, and the Great Inflation, Bilbiie (2013).
Also, I was wondering : why pi_t observations are annualized ? If we look at the second equation : the inflation variable is quarterly and we multiply it by 4 to make it compatible with the quarterly inflation that has been annualized. Why not just simply keep quarterly inflation observations and write : pi_t_obs = pi_t + pi*
I only have the working paper version right now, but there they state that they use the dataset of Lubik/Schorfheide (2004), which used annualized percentage changes.
They indeed use annualized data for inflation, but I do not understand why they do not simply consider quarterly data instead, since the inflation variable is quarterly in the model.
That choice will not affect the estimation results, but it will affect the interpretation of the output. People usually interpret annual inflation, not the quarterly one.
How concretely does it modify the interpretation of the output, if we consider quarterly instead of annualized ? And do we need to take the log of the interest rate in the data ? They are not very explicit on this point.
We are used to annualized inflation numbers in e.g. newspapers. Historical decompositions or variance decompositions of annual inflation are therefore more natural. Logging interest rates is uncommon unless we are talking about gross interest rates.