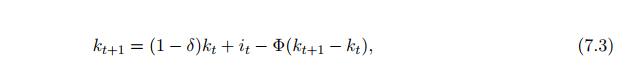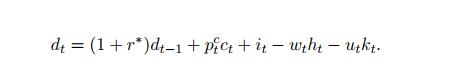Hi,
Imagine we have a multisector production economy where the price of consumption good and investment good are different and final investment good is I_t with price of P^I_t.
So the amount of money invested by the household is P^I_t*I_t while the investment in terms of unit of investment good is I_t.
I wanted to know that the amount of money invested, comes in the production function of firms or its amount in terms of the unit of investment goods, i.e., if K_t comes in the production function and the return of capital is r_t*K_t, what is the correct law of motion for capital: (1 or 2)
- I_t=K_{t+1}-(1-\delta)*K_t
- P^I_t*I_t=K_{t+1}-(1-\delta)*K_t
The first one seems correct, both the right hand side and left hand side are real values. Both I and K are measured in consumption goods, not their nominal values.
In the second equation, you have a nominal value on the left hand side. The right hand side should be nominal as well, I think. It should be in monetary terms. This is hardly done though, and I am yet to see a law of motion for capital in nominal terms.
Thank you for your reply.
Actually I was mixed-up beacuse in Open Macro Book of Schmit-Grohe and Uribe, I think investment is in terms of nominal vaule. (see pictures below from pp 256-7)
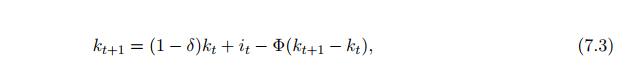
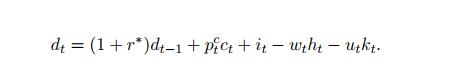
Seems price of investment is normalized to unity here. So nominal value of investment = real value of investment. Investment in law of motion for capital is in real terms. Investment in budget constraint is in nominal terms. But with unit price of investment, I guess it does not matter.
Can we have different numeraires in a model?
in the mentioned book, the numeraire for consumption goods is the importable good, but this way if we look at other equations, the whole tradable good (which is investment) is the numeraire for investment.
As far as I know, the models I have seen so far has just one numeraire for the model economy. Not sure about your confusion, but here is what the book says (kind of):
- Gross investment = importable good.
- And although the price of investment is there in the budget constraint of the household, it has been normalized to one because gross investment (also importable good in the model) is the numeraire for the economy. Other prices are expressed in terms of the price of investment. So for example, the prices stated below eqn. 7.4 are relative prices in terms of the price for investment.
- capital in the law of motion (7.3) is a stock, and not the nominal value of the stock. So as is investment in the law of motion for capital.
- Given that investment is the numeraire of the economy, with its price being normalized to one, its nominal value is same as its real value (measured in consumption units).
I hope this helpful.
It was very helpful. Thank you so much.
Usually, the P_t^I is the relative price of investment (or in a planner’s problem the marginal rate of transformation). It belong in the budget or resource constraint, because it tells you how much investment goods cost relative to the numeraire good. Once the investment good has been produced, it adds one-to-one to the capital stock.
However, many models also feature a marginal efficiency of investment shock. That one shows up in the law of motion for capital, because it determines how efficiently investment goods are translated into installed capital. However, that shocks does not have an immediate budgetary impact and therefore does not show up in the budget constraint.
Thank you so much.
Another question in this regard, the capital rent in such models whith investment good
with a a different price from consumption good, should be: R_t P^I_t K_t or R_t K_t ?
If some other good is the numeraire, and P_t^I is the relative price of investment in terms of the numeraire good, then R_t is also the relative price of capital (i.e., rent) in terms of the numeraire good. Note, if some other good is a numeraire in the model, then all prices are in relative terms with respect to the numeraire. Multiplying two prices, R_t and P_t^I makes less sense, regardless of whether the prices are in absolute or relative terms.
If a model features a marginal efficiency shock in the law of motion for capital, for example, k_{t+1} = (1-\delta)k_t + f(e_t, I_t, I_{t-1}) where f is some function (say, f(e_t, I_t, I_{t-1}) = e_tI_t) and e_t is the marginal efficiency shock, it still does not have any immediate budgetary impact as prof. Pfeifer said, and hence e_t does not show up in the budget constraint.
Hence R_t (not R_t P_t^I) is absolute capital rent if there is no numeraire good in the model, or R_t is capital rent (in relative terms) if the model features a numeraire good.
As always, it depends on your setup. If you define R_t as the physical return to capital in terms of capital goods, then you need to transform it to units of the final good with the relative price. In contrast, if R_t is defined as the return to capital in terms of the final good, then there will be no P_t showing up.