Now I’m getting "Error using print_info
Blanchard & Kahn conditions are not satisfied: no stable equilibrium.
Error in DsgeSmoother (line 133)
print_info(info,options_.noprint, options_);
Error in evaluate_smoother (line 118)
DsgeSmoother(parameters,dataset_.nobs,transpose(dataset_.data),dataset_info.missing.aindex,dataset_info.missing.state,M_,oo_,options_,bayestopt_,estim_params_);
Error in shock_decomposition (line 87)
[oo_, M_, ~, ~, Smoothed_Variables_deviation_from_mean] = evaluate_smoother(parameter_set, varlist, M_, oo_, options_, bayestopt_, estim_params_);
Error in model1.driver (line 801)
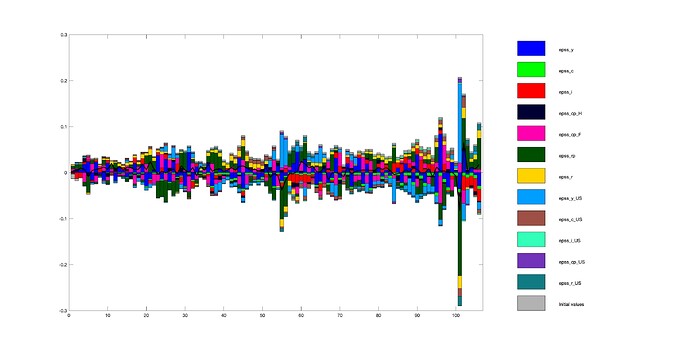
oo_ = shock_decomposition(M_,oo_,options_,var_list_,bayestopt_,estim_params_);
Error in dynare (line 281)
evalin(‘base’,[fname ‘.driver’]);
"
instead when
x=load('model1_results.mat'); M_.params=x.M_.params; M_.Sigma_e=x.M_.Sigma_e; M_.H=x.M_.H;
stoch_simul(order=1, conditional_variance_decomposition=[1,8,32], irf=0) y c i n pi r tot rer;
shock_decomposition(parameter_set=calibration, datafile=dataset1) y c i n pi r tot rer;