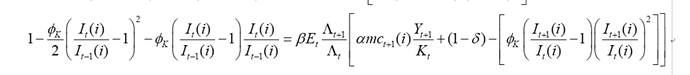BK condition are not satisfied: no stable equilibrium

Stochastic simulations
1

Hi, everyone.

I introduce CES production function to DSGE model, the firm setting follow BMP(2020),when I set the coefficient of adjustment cost of investment phi_K to 0, the model works.

When I set the coefficient phi_K to 10, Dynare reports: Blanchard & Kahn conditions are not satisfied: no stable equilibrium.

image
image457×659 82.2 KB

I think the erro maybe come from the first order condition about capital.

So I would like to know: For my dynare erro, where shold I look for the reasons?

2

Which paper/version exactly are you looking at? Most likely there is a sign error in your implementation that goes away if the adjustment costs drop from the model.

4

Sorry for the delay. Did you solve the issue?

5

Thanks for your reply, Prof Pfeifer.
The paper is “Uncertainty shocks in currency unions (Born ,Müllerand Pfeifer, Decemeber 2020)”, And I derive (3.13) of the paper:

image
image945×132 20.1 KB

I get the first order function of I_t and K_t as following function:

image
image900×99 11.5 KB

I think the function is right, but Dynare reports BK are not satisfied.

6

Usually, it’s

        [name='LOM Capital']
        K(+1)=(1-(delta_0 + delta_1*(u-1)+delta_2/2*(u-1)^2))*K+I*(1-phi_k/2*(I/I(-1)-1)^2);
        [name='Capital Services FOC']
        R_K*(u*K)=alppha*Xi*PF_normalization*(u*K)^alppha*(Z*N)^(1-alppha);
        [name='Capital FOC']
        q = M*(R_K(+1)*u(+1)+q(+1)*(1-(delta_0 + delta_1*(u(+1)-1)+delta_2/2*(u(+1)-1)^2)));
        [name='FOC investment']
        1 = q*(1-phi_k/2*(I/I(-1)-1)^2-phi_k*(I/I(-1)-1)*I/I(-1))
            +M*q(+1)*phi_k*(I(+1)/I-1)*(I(+1)/I)^2;

where

    #M=betta_df*V_C(+1)/V_C;
    [name='Definition marginal utility']
    V_C=eta*a*V_normalization*(C^eta*(1-N)^(1-eta))^(1-siggma)/C;