Hi,
I have got a question about understanding the difference IRFs between calibration and Bayesian estimation. The model dynamics look similar, however, the magnitude is much bigger in Bayesian_IRF compared to calibrated version. I read the document from Professor Johannes Pfeifer, which explains calibrated IRF are from the calibrated parameter (I understand that). However, Bayesian IRFs are mean impulse response, this is the one I don’t quite get it.
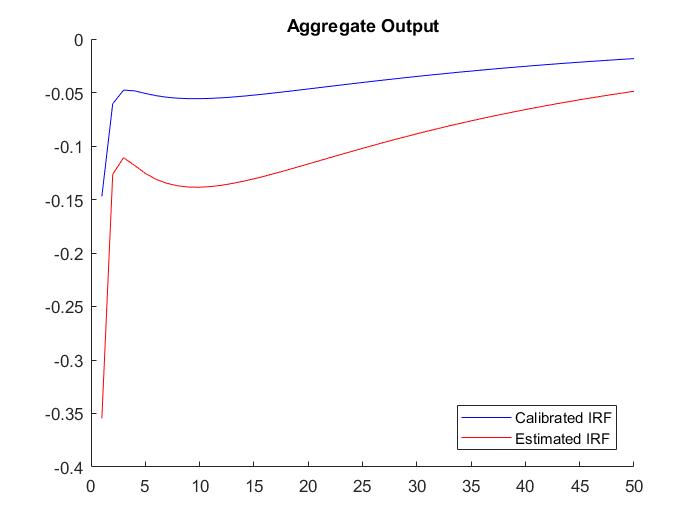
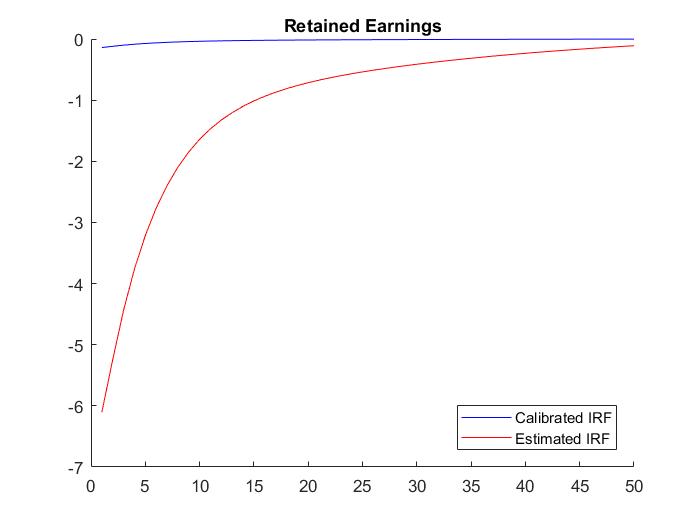
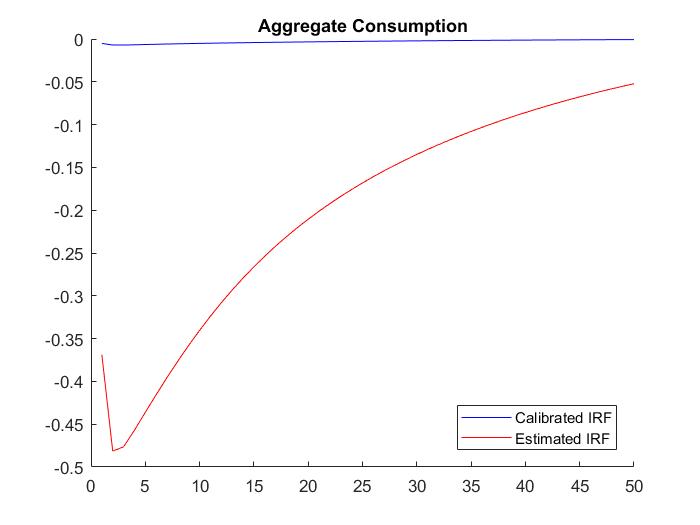
So could anyone help me to clarify this? Specifically, why Bayesian IRFs have bigger magnitude than calibrated IRFs. Please find the attached figures.
Thanks
To which parameter vector did you calibrate the model?
Thanks for the prompt reply.
I am not sure I understand your question clearly. For the simulation of the DSGE model I got, all of the parameters are calibrated (40 parameters in total). For example, discount factor, capital share in the production functions, parameters in the Taylor rule, coefficients in the AR (1) shock processes, and etc.
For the Bayesian estimation, I estimated capital share in the production function, parameters in the Taylor rule and all the parameters in the AR(1) processes.
If the estimated parameters differ from the ones you set in calibration, you will obviously get different IRFs. That’s why I am asking what the relation is between the estimated parameters and the ones you set manually.
I see. Yes, the estimated parameters are indeed different. So if I understand correctly, the difference in the diagram is just simply because the parameters are different. One more question is that why the magnitude is bigger rather than smaller? I have got some diagrams that the estimated IRFs are much bigger than the calibrated IRFs, this raises the question initially.
By the way, all of my estimated IRFs have the similar dynamic with my calibrated IRFs. Does it mean the estimated results confirm the story that explained by the model dynamic? Does it mean the model is good or not or to some extent it is fine?
I am asking this is because these are just estimation, not testing, it seems we cannot argue that the model is good enough. Am I right?
Thanks
You should try to compare the parameters to get a sense of what is going on. Whether the estimated parameters
depends on what your prior allows for. This is the issue of a prior predictive. See Leeper et al (2017) Clearing Up the Fiscal Multiplier Morass
Many thanks for the reply.