Bayesian estimation problem about posterior

Estimation ML/Bayesian estimation
1

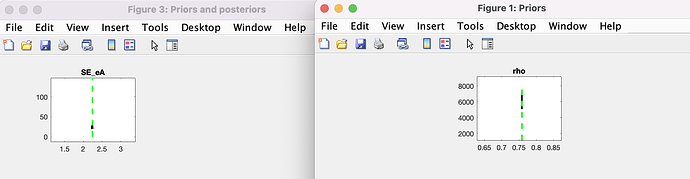
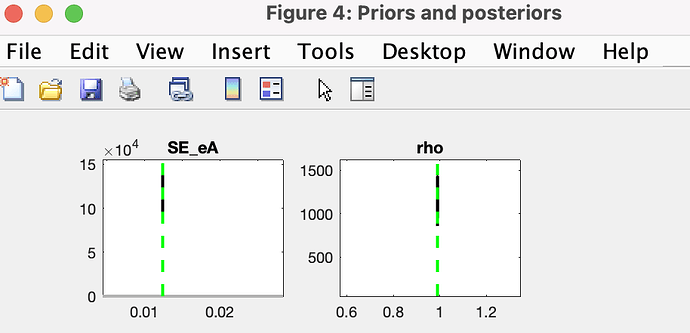
I have a non-linear model to estimate the parameters. The log data are seasonally adjusted and changed by hp-filter. So i construct functions of y_obs and c_obs to fit the original y and c. The problems lie in that the posteriors peek in vertical line like this picture:

image
image1956×508 67 KB

Some key info of the model:
parameters …
rho = 0.75;
model;

tr - tr0 = rho * (tr(-1) - tr0) - (1-rho)( psi_b(b-STEADY_STATE(b)) + psi_y *(y-STEADY_STATE(y)) ) + eTr ;

y_obs = log(y);

c_obs = log(c);

shocks;

var eTr;stderr 0.01;

var eA; stderr 0.01;

var eR; stderr 0.01;

end;

stoch_simul(order=1, irf=200);

estimated_params;
stderr eA, inv_gamma_pdf,0.01,0.005;
rho, beta_pdf, 0.75, 0.15;
% mu, beta_pdf, 1, .04;

estimated_params_bounds;

stderr eA, 0.001, 0.1;

// the following is optional

// Initial values for the parameters in the estimation, pre-set to the optimum..

estimated_params_init;

stderr eA, 0.01;

rho, 0.75;

% mu, 1.0;

end;

rho, .001,.99;

varobs y_obs c_obs; %A

estimation(datafile=Jack_hpfilter, nobs=59, first_obs=1, mode_compute=6,mh_replic=20000, mh_nblocks=2, mh_drop=0.3,forecast=8, plot_priors=1)y_obs c_obs;

2

Without the codes it is impossible to tell. In any case, two-sided HP filtering the data for full information maximum likelihood estimation is rarely ever correct.

4
  1. You are still using a two-sided filter, not a one-sided one.
  2. Your observation equation is wrong. You are matching detrended data to non-mean zero variables. A typical observation in this case equation would be
y_obs = log(y)-log(steady_state(y));
c_obs = log(c)-log(steady_state(c));
5

Thanks for your suggection. After i use
y_obs = log(y)-log(steady_state(y));
c_obs = log(c)-log(steady_state(c));
The pictures still shows the same problem. By the way, i actually use the two-sided hp filter to get the data of T by 1…T and roll it to the end? Is the idea wrong compared to Stock and Watson(1999)? Or are there some sample codes about one-sided hp filter?
Jack_hpfilter.m (2.2 KB)

image
image914×442 23.7 KB

6
  1. Dynare ships a one_sided_hp_filter.m file you should use.
  2. The problem is that rho runs into the upper bound. You need to understand why the data favors a corner solution.
7

I have tried one-sided-hpfilter.m. The result shows the same estimation of data after filtered.

image
image454×714 13.9 KB
. Thanks for your suggestion. And i will check why rho hits the upper bound. Thanks again.