Bayesian estimation of variant of NK baseline model

Estimation ML/Bayesian estimation
1

Dear all,

I am trying to estimate a NK DSGE model that is quite similar to the NK baseline model of FV(2010) with respect to the model structure. The equilibrium conditions are in their non-linear representation and not log-linearised.

I specified my prior distributions in line with the previous literature. As an example:

sig_z (std. neutral technology shock) and sig_nu (std. investment specific technology shock)
sig_z, 0.1, 0, Inf, inv_gamma_pdf, 0.1, 0.02;
sig_nu, 0.1, 0, Inf, inv_gamma_pdf, 0.1, 0.02;

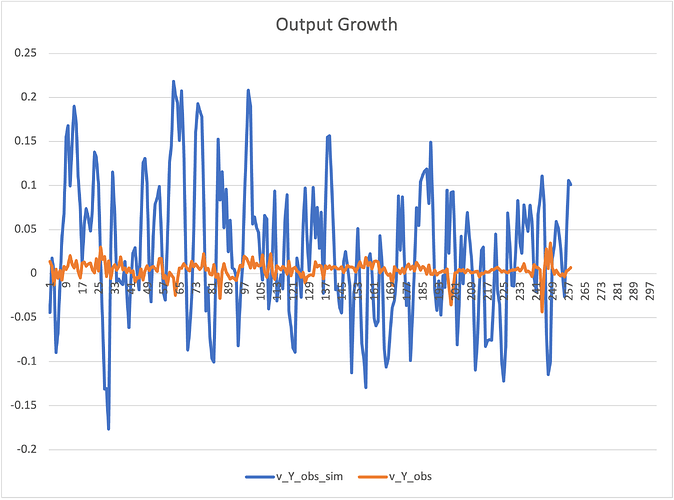
If I estimate my model on simulated data, estimation works well and all the diagnostics (mode_check plots, convergence, etc.) look reasonably well. However, if I use observed US data, estimation fails. In particular, I cannot find valid posterior modes of the parameters. Comparing simulated with observed data shows that the model implied data is much more volatile. Below is a graph that shows the comparison for QoQ per capita GDP growth (not annualised, in model terms, not in perc. points, not demeaned). My observation equations are based on Pfeifer (2014). For instance, for GDP growth I use:

Y_obs = log(Y_{t}) - log(Y_{t-1}) + log(mu) + sig_Y*eps_Y_ME,

where mu represents the gross growth rate of output along the BGP and the term on the right incorporates a measurement error.

Do I have to reduce the std. of my shock processes to reduce the volatility of my model implied dynamics such that estimation will work on less volatile observed data? Or do I most likely have a problem with the model anywhere else since I would need to deviate from priors often specified in the literature?

Thank you!

OutputGrowth
OutputGrowth2195×1627 378 KB

2

At which point in the parameter space did you simulate the model? And what do the mode_check-plots indicate on the actual data?

3

I used the initial values of my priors (also my prior mean) to simulate the model. The mode-check plots on the actual data indicate prior bound issues for some of the parameters (for example, the parameter on the inflation gap hits the lower bound at 1) and for others the posterior mode is not at the maximum of the log-posterior curve. The problem doesn’t vanish if I use prior_trunc = 0.

4

The prior mean may not be a good starting point as it implies too much volatility. Without investigating the issue in more detail, it is impossible to provide further advice.