Are these IRFs correct?

Stochastic simulations
1

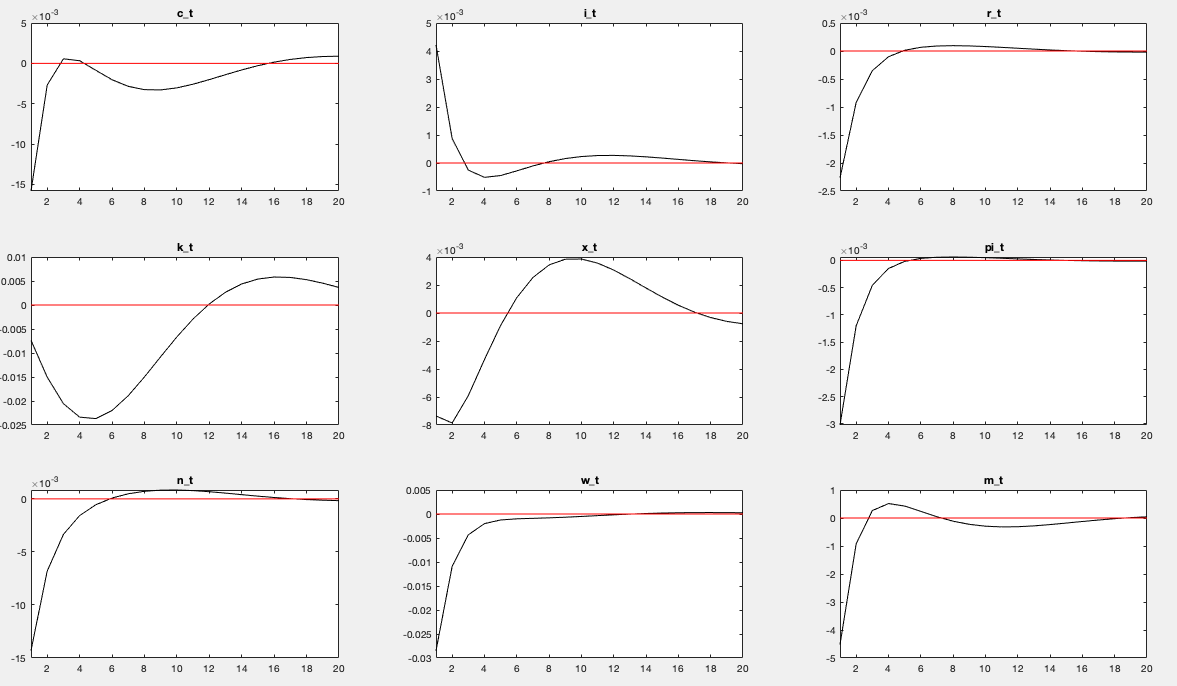
I’m working with NK-Calvo model incorporating capital adjustment costs and investment adjustment costs (not simultaneously), the latter adj. costs as explained in Sims’ class notes (section 2.3). Particularly for example, when I use the CEE (2005) investment adjustment costs, these are the responses from a Taylor rule shock:

image
image1177×686 17.7 KB

Which seem kind of odd to me. I’ve read some of the posts in this forum that treat the “oscillating” behavior of IRFs and its relationship (sometimes) with wrong timing. In that sense, there arise two questions. First, if the irfs were to be wrong, it’s almost certain (I think) that the timing misspecification comes from investment/capital’s dynamic motions set-up. Focusing only in the case of CEE, they specify the capital law of motion as (see eq. 3.21):

k_{t+1}=(1-\delta)k_{t}+\frac{\phi}{2}\left(\frac{I_t}{I_{t-1}}-1 \right)^2+I_t

Now, what I did in order to be congruent with Dynare’s timing convention, is rearranging this equation to:

k_{t}=(1-\delta)k_{t-1}+\frac{\phi}{2}\left(\frac{I_t}{I_{t-1}} -1 \right)^2+I_t

And then proceeded to find first order equilibrium conditions using the latter. Is this procedure right or did I miss something important?

Similarly, capital adjustment costs would convert from:

k_{t+1}=I_t+(1-\delta)k_t-\frac{\phi}{2}\left(\frac{I_t}{k_{t}}-\delta\right)^2k_t

to

k_{t}=I_t+(1-\delta)k_{t-1}-\frac{\phi}{2}\left(\frac{I_t}{k_{t-1}}-\delta\right)^2k_{t-1}

Is this also right? (the irfs reported by me come from the timing that I think is correct, the second ones)

Now in the other hand, checking some of the figures reported in the mentioned CEE paper I noticed that indeed they obtain oscillating irfs from theoretical model, maybe suggesting that the irfs I get are not wrong (I’m not comparing signs or the exact irfs due to we’re using at least different calibrations, I’m only checking the fact that those are also oscillating), see e.g.

image
image707×889 41.9 KB

To summarize, I’d be grateful if you may give me some comment in determining if my irfs are right in light of the described procedure that I followed with cap/inv laws of motion, particularly if you may confirm that the mentioned procedure is correct but irfs are not correct, then I’ll check my math and code. However, if it turns out to be that all that is correct, and therefore this oscillating irfs are ok, I’d be grateful if you could explain me the economic nature of such behavior (if in a first instance you could answe.

Thanks!

PD: Note that this behavior not only occurs in TR shocks but also in other types of shocks.

nkm_cap_inv_adj_cost_steadystate.m (1.8 KB)
nkm_cap_inv_adj_cost.mod (5.1 KB)

2

Your timing changes are exactly right. They should be done that way. Basically, everything that you know at the beginning of time period t should be denoted as t-1 in Dynare (and capital is usually the only one you need to change).
Your IRF above comes from this modified one? What I know is (from one of my friends’ paper, actually) with both capital adjustment and preference habit formation, you might get something like this.

1 Like
3

Thanks for your answer. Indeed, my reported irfs come from specifying the model in the way I specified in the second instances. In this case I didn’t include habit formation, but seems like inducing these kind of stickiness makes irfs like that? In the other hand, in empirical irfs from VARs it’s more or less common to see such kinds of behavior, is that right?

4

What you have here is overshooting, which is extremely common. Oscillations from wrong timing usually look very different:

from Irregular movements in dynamics with an investment adjustment costs model

1 Like
5

By overshooting you mean something similar to exchange rate overshooting? May you refer me some literature to understand this better in DSGE context? Thanks!

6

The is not a standing term. I used the term to denote that in many models the return to the steady state immediately, but rather they overshoot the long-run level and then return.
Take a TFP shock in the RBC model. As a consequence, investment increases above steady state and the capital stock increases. For capital to go back to steady state, investment usually needs to fall below steady state at some point, before then finally returning to steady state.

1 Like