In the paper: SGU2006, Optimal Simple and Implementable Monetary and Fiscal Rules: Expanded Version (snapshot above), the welfare comparison is based on the premise that “the non-stochastic steady state is the same across all policy regimes”.
Is this equivalent to say that: if I introduce a policy instrument into the model, but some steady states of the model are therefore changed, then initial states of different policy regimes are no longer the same. Welfare comparison conditional on the initial state is invalid??
If the answer is “yes, equivalent”, can I still compare the welfare by unconditional indicators, for example, oo_.mean(welf) ? I saw many papers just compare various scenarios in a very “natural” way, but when I do it by myself, I guess this may be a problem.
Sorry for my stupid question.
The answer always depends on what you are trying to do. Conditional welfare is something used when you ask whether a change in a policy regime is beneficial. In that case, you would start at or somewhere close to the steady state of the old regime and this is the starting point for the implementation of the new policy. If the steady states in the new regime is different, then you would need to compare welfare at the steady state of the old regime.
Unconditional welfare in contrast is not concerned with transition behavior. Policies happen in two different economies that have been running for a long time. Now you compare them.
1 Like
Thank you for the reply. I’m turning your words into codes 
Sorry I have another fairly naive question on that paper (and on many other peers).
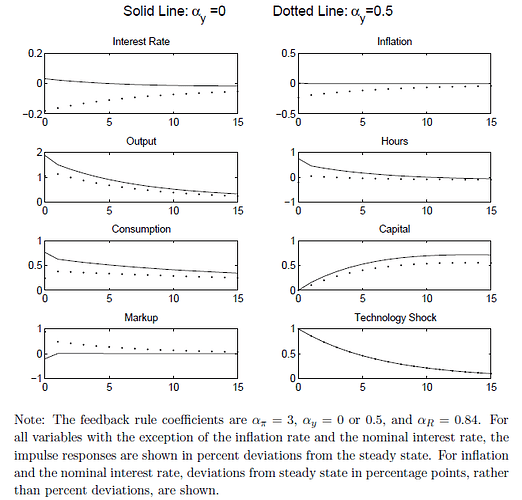
In Figure 3, authors show IRFs of OSR (\alpha_y=0) and the usual Taylor rule (\alpha_y=0.5).
For Interest Rate and Inflation, first two subplots, as well as the second to last Markup, I can see OSR is definitely superior to Taylor. SGU seem to exclusively analyze them.
But for Output, Hours, and rest real terms, the “volatilities” or percent deviations of OSR are larger than Taylor. If I change to other variables, results are similar.
Is OSR only optimal in terms of utility-based welfare? If I alter the criterion, say “volatility minimization”, can I conclude Taylor is superb?
Broadly, is there any paper characterizing a “universal” optimal rule, not only max the welfare, but min volatility as well? Or for any rule, optimality under one criterion is at the expense of being suboptimal under alternate criteria?
Sorry, my experience on the interpretation of IRFs is rather limited. If, for instance, I generate 10 subplots. 2 of them favor my claims and the remaining are not. Shall I follow SGU that only speak something about the 2 subplots?
Thank you for your tolerance.
Whenever you want to say something about optimality, you need to have an objective function. If your objective is agents’ welfare then a particular policy will be optimal (essentially the utility function will dictate the weights on the levels and volatility of the variables entering utility).
If you now use a different objective with an arbitrary weighting, then a different policy may be optimal. But given that variables and weights in the objective could be anything, there is of course no general rule on which policy will be best according to this metric.
I want to find the effect on welfare of introducing a certain policy. However, once the policy is in place, the deterministic steady state of the model is different.
I don’t really understand what this sentence I cited means, i.e., how can I compare welfare at the steady state of the old regime? Does this mean simulate the model with policy and a different deterministic steady state starting at the “old” steady state of the model without policy? However, this might not even be possible if the deterministic steady state of the old model/regime is not an equilibrium of the new model/regime.
At each point in time, there are values for the predetermined state variables you need to take as given. All control variables are functions of the state variables. Comparing conditional welfare involves evaluating the policy functions of the new regimes at the values of the old states. That will always be an equilibrium.
Thank you very much for the clarification!