Adaptive learning and convergence

Estimation ML/Bayesian estimation
1

Dear dynare community,

I am estimating the model of Rychalovska et al. (2016) under rational expectations and under adaptive learning (minimum state variable) using the code provided by Slobodyan and Wouters that is running on dynare 3.64.
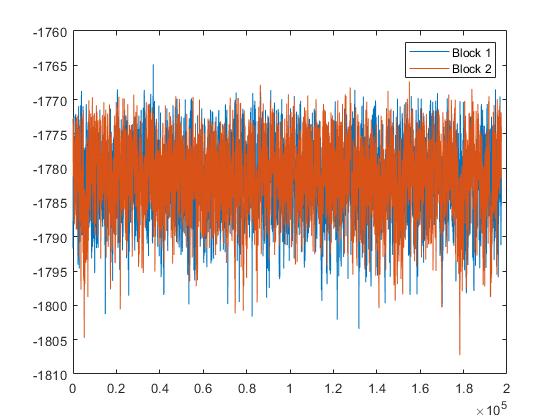
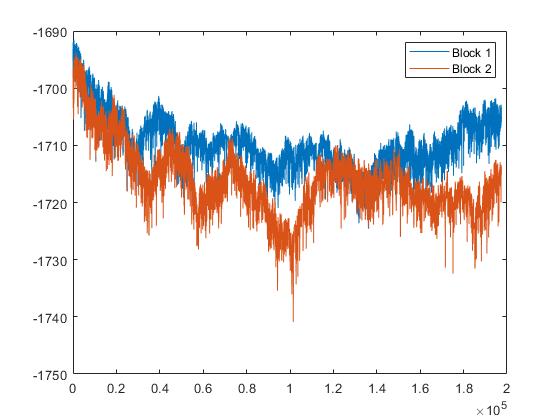
In both cases, I run two blocks of 200k realizations (attached graphs plot the realization of each block). In the case of rational expectations, it seems that the MH reaches convergence. In the case of AL the realizations make the likelihood vary quite a lot. Then, if I evaluate the AL model in any accepted realization for the parameters seems that the fit is better than when I do the same for the RE model. Nevertheless, when it comes to evaluating the model in the posterior mean the AL model gets a much worse likelihood.
My questions are:
Is this a consequence of the no convergence in the AL model?
In such a case, should it solve the problem to add sufficient realization to make the AL model converge?

Thank you very much in advance
RE AL

2
  1. You cannot compare models based on the posterior density. It does not account for degrees of freedom used. That’s what the marginal data density is for.
  2. The bottom picture shows clear signs of non-convergence. This will make any inference likely wrong. At a minimum, you need a much longer chain.