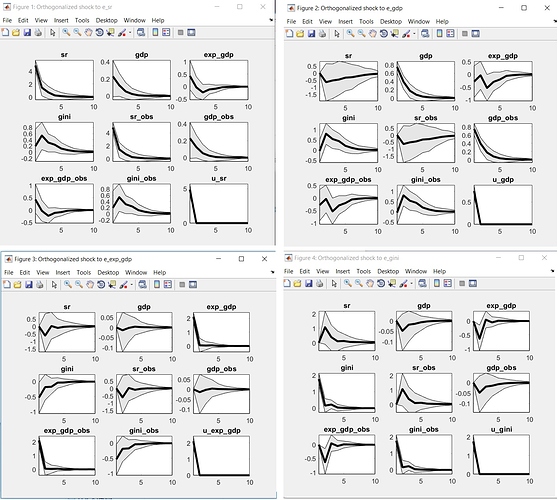
A question about Bayesian IRFs

BVAR
1

Hello,

I tried to estimate a 4-variable BVAR but I got rather strange IRFs, the HPD interval is large and then it decreases, shouldn’t it be the opposite? I’m using annual data so I have only 41observation.

Please see attached for the plots.

Bayesian_irfs
Bayesian_irfs.jpg1422×1273 342 KB

Thank you for your help.

2

Hello,

I would really appreciate some help on this if anyone can help? Do you think there is something wrong with the model or it is ok to get the HPD interval like the one above? Also, does anyone know if there is a way to get accumulated IRFs in Dynare, as my variables are differenced?

Many thanks in advance for the help!

3
  1. A stationary VAR will always return to its unconditional mean. If the coefficients governing that mean like the constant term are very precisely estimated in comparison to the parameter governing the dynamics, you can get a picture like the one you have.
  2. That being said, it is rare to have the long-run response that precisely estimated (unless you have an extremely tight prior or a lot of data).
  3. To get levels from growth rates, you would have to cumulate the saved IRFs yourself.
4

Thank you very much for your help. I also have an issue with Modified Harmonic Mean when I try to estimate this model with 8lags, it says: “the support of the weighting density function is not large enough” and the posterior marginal density is -infinite, but it gives me the results and plots of IRFs. I tried to use Hessian or prior variance but it didn’t help, in the latter case the convergence graphs were really bad. Do you know why this may happen, as there is no this issue if I consider 5lags?
Another question is about priors: when I estimate the same model for another country, I get this for two of the priors (the priors are obtained from the estimates of independent AR(1) processes):

image

How can I fix this?

Thanks in advance for all the help.

5

This suggests problems with the estimation.
The plot you show indicates that some coefficients run towards a unit root. This may be a problem as the VAR will not be stable anymore.