Do we calculate the derivatives for all variables in the Lagrangian or just for some specific variables?
Only for the control variables. Agents do not optimize with respect to the exogenous variables, for example.
When I read some studies, I find that they optimise just for some variables not for all control variables. Another exmple is when they derive for a variable with time script (t+1) instead of (t). What is the reasons behind this kind of derivation?
If I may contribute for the second part of the question with the hope of being corrected: people derive with respect to t+1 instead of t probably because the t variable is a state variable. For example, at time t, we can decide consumption level c_t. However, the machines of today, so capital k_t, are given. You cannot maximise something that is already given. You can only choose the capital for the next period k_{t+1}. Understanding the difference between state and control variable is extremely important for dynamic programming.
- Do you have an example where the derivative is not taken for all control variables? Note that control variables is always from the perspective of the economic agent. In competitive models, agents are price takers and don’t optimize with respect to prices. They will be pinned down by the market clearing conditions.
- As @DiegoHidaFl correctly outlined, if you use the stock at the beginning of period notation, the derivative is taken with respect to t+1 values due to variables at time t being predetermined.
If I understand, that means I must calculat the derivatives for all the control variable except the price.
Are all those FOC’s (derivatives) written down in dynare code ? or just we combine them to get some special ones ?
The price is not a control variable. To be precise, you need to enter all equilibrium conditions except for the transversality condition. Have a look at papers defining such an equilibrium precisely. They will state that you need the FOCs for firm and households as well as the market clearing conditions that will determine the prices.
You ultimately need as many equations as endogenous variables. You can combine FOCs as long as you eliminate variables by doing so. But that is not required.
What are the equilibrium conditions and what about the market clearing conditions ?
That differs from model to model. Market clearing conditions are usually equilibrium conditions because market clearing is the constitutive feature of most equilibrium concepts.
Can you please give me more details about this point ?
Please look at any graduate textbook. They will define equilibrium concepts.
Thank you Professor
For example, how the FOC’s of this problem are calculated
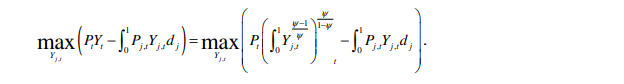
Have a look at
HI, I would like to understand what you mean by capital K_t is already given.
This is the crucial point. You have to understand the difference between control and state variables. State variables are given. Today I have x amount of machines k_t. Because they need to be installed or built or whatever, the decision of today will affect the quantity of capital only tomorrow, k_t+1.
There are other state variables, for example, prices which the household cannot control, but behind there is another reasoning (which is that households are price takers).
In the end, it depends on the setup of your model, with respect to what agent you are deriving the FOCs, etc. but you will understand that after deriving yourself the examples we have provided during the whole thread and looking at graduate macroeconomic textbooks.
WHAT DOES STATE VARIABLE MEAN ? AND PLEASE CAN YOU EXPLAIN MORE THE EXAMPLE OF CAPITAL HOW THE the decision of today will affect the quantity of capital only tomorrow, k_t+1?
Furthermore, why we consider the K_t as given ?