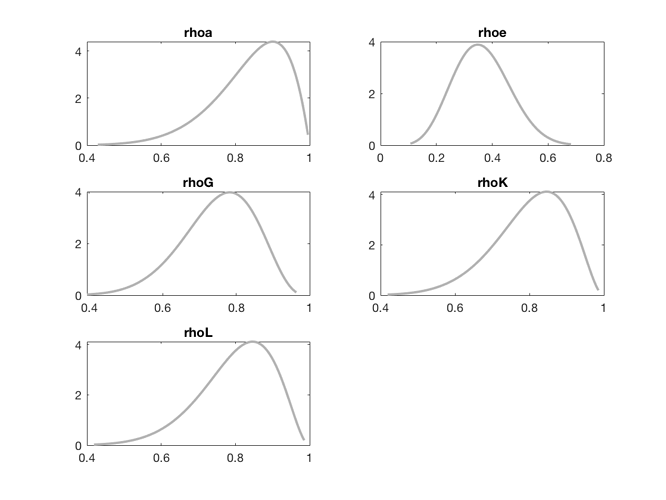
Professor Pfeifer, thank you for the response. The issue persists when I change the prior mean of rhoK to 0.8 - as shown below, none of the priors are asymptotes now, yet the acceptance rate for MCMC remains to be 0. I read in this post that the problem might be with the data, but I am not entirely sure after reading all the relevant posts about acceptance rates. What do you think the issue might be in this case? Thanks again.