Hi!
I am just a basic learner of dynare. I want to create a time series of endogenous variables relative to their steady states based on Smets and Wouters (2007) paper. I got confused after going over several discussions in the Dynare forum. Some people are using stochastic simulation while others are recommending estimation for that purpose. Which method do you suggest to me so that I can plot the deviation of all the endogenous variables from their steady states based on the Smets and Wouters model?
Thank you!
What exactly do you want? Artificial simulated data from the model? Or estimates of unobserved variables based on the model and the set of observed data?
Hello,professor!
Thanks for replying to my question. I want to get artificial simulated data from the model so that I can see whether those simulated endogenous variables can match the real data from 1966Q1 to 2020Q1. I have done simulation a couple of times in dynare. But I do not know the matching process from simulated date within a specific period of time like some literature report. Thanks once again for your time!
Your answer is still not well-defined. If you want to see how a model matches the data, how do you pick the shocks? If you use the shocks from the Kalman smoother, they will alway perfectly explain the observed data used to run the Kalman smoother.
Thank you professor. Yes, it seems I am confused between the model and data thing. What I understood from your response is that simulating the model after updating the standard deviation of the shock processes with the posterior standard deviations, is one of the ways to compare the endogenous variables in model and data? Thanks once again for your time to make me clear.
No, that is not what I was saying. You need the realization of shocks at each point in time, not just the standard deviation of their distribution.
Dear professor Pfeifer;
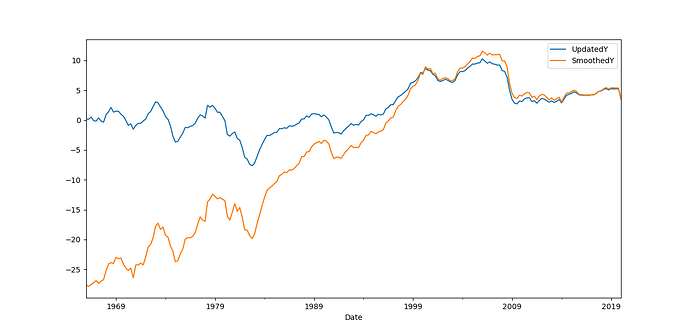
Thanks for your responses. I hope you are doing well. I followed your estimation code in Smets and Wouters (2007). I want to study the deviation of endogenous variables from their steady states over time. I plotted smoothed output (Y) and updated output (Y) obtained from the estimation, which is attached to this post. For me, the time series of smoothed variables seems to be a little bit awkward relative to that of Updated Y, as the initial deviation is huge in the former case. At some point in this forum, I found that smoothed variables better define the path than the updated variables. Would you provide me some insights so that I can use the right time-series for my cause?
Thank you once again for your time.
Nirajji
The smoothed shocks use the information of the whole sample until the end, the updated ones only the information up to the current period. Due to the larger information set, we prefer the smoothed variables unless we do real-time exercises.
Thank you, professor very much for your answer. I now understood.