Question about the retailer model

aibenaimer1 · May 13, 2018, 7:33am

Dear all：
When I attempt to a modeling of price addition of the retailer, question appears.It’s not a complicated problem.But I can’t find the problem, I’m tortured. Can someone can find out the error in my model? I would appreciate it very much.
%E6%8A%80%E6%9C%AF%E5%86%B2%E5%87%BB
deleverage12.mod (3.1 KB)
deleverage13.mod (2.7 KB)
model.pdf (113.6 KB)

%----------------------------------------------------------------
% 1. Defining variables
%----------------------------------------------------------------

var y ch ce w l pi r rk k i x
a ;

varexo eps_a ;

parameters alpha gamma sigmma delta beta theta nu omega lambda
kappa_r kappa_y kappa_pi rho_a rho_pi rho_r chi rho_x ce_ss s_ss
phi_f_ss phi_p_ss l_ss a_ss mu_p_ss x_ss r_ss rf_ss rk_ss
w_ss k_ss i_ss y_ss f_ss n_ss d_ss cb_ss ch_ss ;

alpha = 0.5 ;
gamma = 1 ;
sigmma = 1 ;
delta = 0.025 ;
beta = 0.99 ;
theta = 0.85 ;
nu = 0.97 ;
omega = 0.002 ;
lambda = 0.19 ;
rho_a = 0.5 ;
rho_x = 0.5;
rho_pi = 0.5 ;
rho_r = 0.5 ;
kappa_r = 0.8 ;
kappa_y = 0.5 ;
kappa_pi = 1.5 ;

phi_f_ss = 10 ;
phi_p_ss = 2 ;
l_ss = 1/3 ;
a_ss = 1 ;
mu_p_ss = 1;
q_ss = 1;
x_ss = 1.1;
r_ss = 1 / beta ;
rf_ss = (1 - nu * r_ss - phi_f_ss * omega )/ (phi_f_ss * nu ) + r_ss;
rk_ss = 1 / beta - (1 - delta) ;
k_ss = (rk_ss * x_ss / alpha)^(1/(alpha - 1 ) ) * l_ss ;
w_ss = (1 - alpha ) * (alpha^alpha / rk_ss^alpha)^(1/(1-alpha))/x_ss ;

i_ss = delta * k_ss ;
y_ss = a_ss * k_ss^alpha * l_ss^(1 - alpha);

s_ss = k_ss / phi_p_ss ;
f_ss = k_ss - s_ss ;
n_ss = f_ss / phi_f_ss ;
d_ss = f_ss * (phi_f_ss - 1) / phi_f_ss;
ce_ss = y_ss/x_ss + f_ss - i_ss - rf_ss * f_ss - w_ss * l_ss;
cb_ss = (1 - nu) * (rf_ss * f_ss - r_ss * d_ss);
ch_ss = y_ss - cb_ss - ce_ss;
chi = ch_ss^(-sigmma) * w_ss / l_ss^gamma ;

%----------------------------------------------------------------
% 3. Model
%----------------------------------------------------------------

model(linear);

%%%%%%%%%% HOUSEHOLD PROBLEM %%%%%%%%%%%%%%%%%%%%%%%%%%%
//1. labor supply equation
w = sigmma * ch + gamma * l ;

//2. Euler equation

sigmma * ch = - sigmma * ch(+1) + (r - pi(+1) );

%%%%%%%%%% FIRM PROBLEM %%%%%%%%%%%%%%%%%%%%%%%%%%%
//3.Entrepreneurial Resource Constraints
ce_ss * ce + w_ss * l_ss * (w + l) + i_ss *( i ) = y_ss / x_ss *( y - x ) ;

//4. Capital accumulation equation
k = (1 - delta) * k(-1) + (i_ss / k_ss) *( i );

//5. Production Function
y = a + alpha * k(-1) + (1 - alpha) * l ;

//6. Entrepreneurial Euler equation2
ce = ce(+1) - (1/sigmma)*(rk(+1) * rk_ss /(rk_ss + 1 -delta) );

//7. wages condition
w = y - l - x ;

//8. Rate of return on capital
rk = y - k(-1) - x ;

//9. philipus curve
pi = beta * pi(+1) - (1 - theta)*(1 - beta * theta) * x / theta ;

%%%%%%%%%% BANK PROBLEM %%%%%%%%%%%%%%%%%%%%%%%%%%%

//10. resource equation
y = (ch_ss/y_ss) * ch + (ce_ss/y_ss) * ce + (i_ss/y_ss) * i ;

//11. Taylor Rule
r = kappa_r * r(-1) + (1 - kappa_r) * (kappa_y * y + kappa_pi * pi) ;

//shocks
a = rho_a * a(-1) + eps_a;

end;

initval;

y=0.0;

ch=0.0;
w=0.0;
l=0.0;
pi=0.0;
r=0.0;
rk=0.0;

ce=0.0;
k=0.0;

i=0.0;
x=0.0;
a=0.0;

end;

resid(1);
steady;
check;
model_diagnostics;

shocks;
var eps_a =0.01^2;

end;

stoch_simul(irf=40,order=1,hp_filter=100,periods=2100)y ch pi r rk i x ;

jpfeifer · May 15, 2018, 4:59pm

Are you sure your Phillips Curve is right? Usually there is plus and not a minus in front of marginal costs.

aibenaimer1 · May 16, 2018, 2:57am

Professor jpfeifer, thanks for your reply. Xt is the gross markup of retail goods over wholesale goods. I indeed didn’t have a formula to deduce by myself. But Bernanke, Gertler,Gilchrist(1999)“The financial accelerator in a quantitative business cycle framework” , Iacoviello, Matteo(2005)American Economic Review “House Prices, Borrowing Constraints, and Monetary Policy in the Business Cycle”, and in some other articles , Phillips Curve is the same as in my model. I can’t find the problem, so I can only search help from you. Are there any other possible questions?

jpfeifer · May 17, 2018, 6:19am

I see. Then I also don’t know what is going on. Sorry.

aibenaimer1 · May 17, 2018, 2:26pm

Thanks for your time

aibenaimer1 · May 24, 2018, 6:36am

@jpfeifer Professor jpfeifer, After all kinds of attempts, will I be wrong in my steady state?This may be the only possible reason

jpfeifer · May 24, 2018, 7:44am

That can of course be the reason. You should check whether the size and sign of the values makes sense.

aibenaimer1 · May 24, 2018, 7:56am

I wrote a basic NK model，Recalculated the steady-state value and did not assign labor to 1/3.
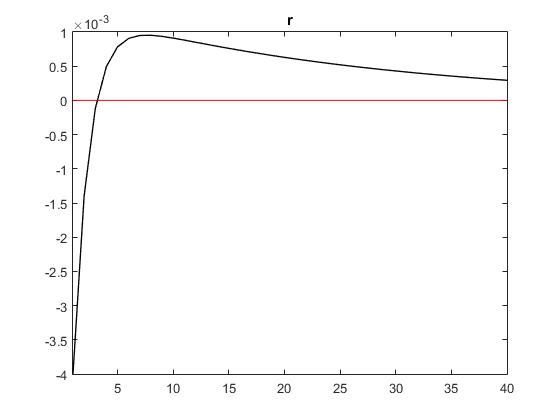
Why Monetary%20policy%20shocks can r start from zero or one? like the picture. The steady state value of the marginal cost is (GAMMA - 1)/ GAMMA ？GAMMA is the substitution of elasticity，Is it right?

%----------------------------------------------------------------
% 1. Defining variables
%----------------------------------------------------------------

var y ch w l pi r rk k i mc
a mu_r ;

varexo eps_a eps_r ;

parameters alpha gamma sigmma delta beta theta GAMMA
kappa_r kappa_y kappa_pi rho_a rho_pi rho_r rho_x
l_ss a_ss r_ss rk_ss
w_ss k_ss i_ss y_ss ch_ss ;

alpha = 0.5 ;
gamma = 1 ;
sigmma = 1 ;
delta = 0.025 ;
beta = 0.99 ;
theta = 0.75 ;

rho_a = 0.5 ;
rho_r = 0.5 ;
kappa_r = 0.5 ;
kappa_y = 0.5 ;
kappa_pi = 1.5 ;
GAMMA = 11 ;
mc_ss = (GAMMA - 1)/ GAMMA ;
a_ss = 1 ;
r_ss = 1 / beta ;
rk_ss = 1 / beta - (1 - delta) ;
w_ss = (1 - alpha ) *mc_ss^(1/(1-alpha) ) (alpha / rk_ss)^(alpha/(1-alpha)) ;
y_ss = ( rk_ss/(rk_ss - alpha * deltamc_ss ) )^( sigmma /( sigmma + gamma ) ) * ( w_ss * ( w_ss/ ((1-alpha)*mc_ss) )^gamma )^(1 /( sigmma + gamma ) ) ;
k_ss = mc_ss * alpha * y_ss / rk_ss ;
i_ss = delta * k_ss ;
ch_ss = ( 1 / y_ss^(gamma/sigmma )) * ( w_ss * ( w_ss/ ((1-alpha)mc_ss) )^gamma )^(1/sigmma ) ;
l_ss = mc_ss * (1-alpha) y_ss/w_ss;

%----------------------------------------------------------------
% 3. Model
%----------------------------------------------------------------

model(linear);

%%%%%%%%%% HOUSEHOLD PROBLEM %%%%%%%%%%%%%%%%%%%%%%%%%%%
//1. labor supply equation
w = sigmma * ch + gamma * l ;

//2. Euler equation

sigmma * ch = - sigmma * ch(+1) + (r - pi(+1) );

%%%%%%%%%% FIRM PROBLEM %%%%%%%%%%%%%%%%%%%%%%%%%%%
//3.Entrepreneurial Resource Constraints

//4. Capital accumulation equation
k = (1 - delta) * k(-1) + delta *( i );

//5. Production Function
y = a + alpha * k(-1) + (1 - alpha) * l ;

//6. Entrepreneurial Euler equation2
ch = ch(+1) - (1/sigmma)*(rk(+1) * rk_ss /(rk_ss + 1 -delta) );

//7. wages condition
w = mc + y - l ;

//8. Rate of return on capital
rk = mc + y - k(-1) ;

//9. philipus curve
pi = beta * pi(+1) + (1 - theta)*(1 - beta * theta) * (mc ) / theta ;

%%%%%%%%%% BANK PROBLEM %%%%%%%%%%%%%%%%%%%%%%%%%%%

//10. resource equation
y = (ch_ss/y_ss) * ch + (i_ss/y_ss) * i ;

//11. Taylor Rule
r = kappa_r * r(-1) + (1 - kappa_r) * (kappa_y * y + kappa_pi * pi) + mu_r ;

//shocks
a = rho_a * a(-1) + eps_a;
mu_r = rho_r * mu_r(-1) + eps_r;

end;

initval;

y=0.0;

ch=0.0;
w=0.0;
l=0.0;
pi=0.0;
r=0.0;
rk=0.0;

k=0.0;

i=0.0;

a=0.0;

end;

resid(1);
steady;
check;
model_diagnostics;

shocks;
var eps_a =0.01^2;
var eps_r =0.01^2;

end;

stoch_simul(irf=40,order=1,hp_filter=100,periods=2100)y ch pi r rk i k ;

aibenaimer1 · May 24, 2018, 8:16am

I’m sorry I didn’t say it clearly, When there is monetary policy shock, Why interest rates" r" start under 0? r should start above the 0 axis.I have confirmed that there should be no error in the steady state value. I really could not understand it.@jpfeifer
Monetary%20policy%20shocks

aibenaimer1 · May 24, 2018, 12:08pm

@jpfeifer Professor jpfeifer, Can you give me an example of a basic NK model code including capital? Then I can find a mistake than my face contrasting to it.
It’s the simplest NK model. I really can’t find out where the mistake is by myself.

aibenaimer1 · May 25, 2018, 1:45am

@jpfeifer There are similar problems in the Forum. If there is no mistake in my model， monetary policy shocks can ruduce the R, or software has bug？
Can you help me to point it out？and how to explain？

jpfeifer · May 25, 2018, 8:41am

See Positive monetary policy shock with nominal interest rate falling?

aibenaimer1 · May 25, 2018, 11:00am

Thank jpfeifer, I’ve seen this explanation， so maybe I did not do nothing wrong，Is it right?
Contractionary policy shocks is not necessarily greater than 0 for interest rates ？ As “The central bank then reacts to lower output and inflation endogenously by lowering the nominal interest rate. If the response is strong enough, it overcompensates the initial increase due to the shock. ”
I’m not sure I did the right thing, so I want to make sure.

jpfeifer · May 28, 2018, 9:24am

I did not build your model and am not familiar with it. I can only point you to general theoretical results. But it is your job to check whether this applies to your model.

aibenaimer1 · May 29, 2018, 1:13am

Thank jpfeifer, I’ll try it.

Pang · October 3, 2018, 4:22pm

I also met this problem before. your results is right, this paper may be helpful for you .
On the Mechanics of New-Keynesian Models written by Peter Rupert

aibenaimer1 · October 5, 2018, 11:27am

@ [Pang] Thank you for your advice. But I still can’t find out where the problem is. I’m really not sure if I’m doing the right thing. I’ve checked the model over and over again. There should be no mistakes?
Do you have a code similar to mine, the simplest one is OK?I will be very grateful.