Hi,
I have Bayesian estimated my model and have acquired a standard deviation of 0.0117 for the shock that I am interested in explaining and analyzing. When I use stoch_simul and use stderr 0.0117; it will result in explosive dynamics error and asks to use pruning. When I reduce the standard error of the shock to 0.001 then it can simulate the and give results without pruning. My question is if I want to submit my research in a journal, can and should I use pruning or I should the maximum value of standard error that results in no explosive dynamics and therefore does not require pruning?
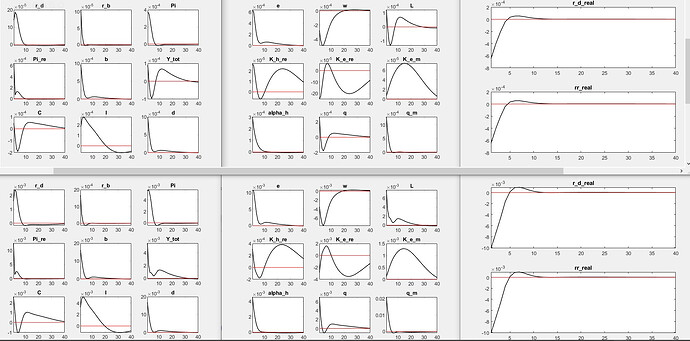
I have included the results of the model with the estimated standard deviation shock with pruning and the model with very low standard deviation shock without pruning below. The first row is the one with sd=0.001 and no pruning and the second row is for the estimated sd=0.0117 + pruning. As you can see the simulated total ouput (Y_tot) and labor (L) have noticeable difference between the two and change the explanation of the effects of the shock.
Thank you in advance.
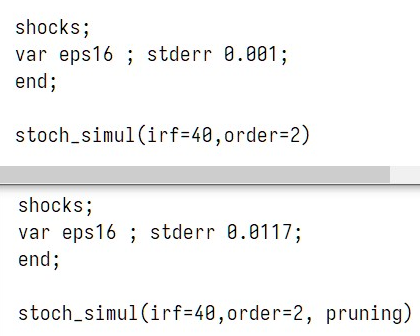
The code I use for each one:
At higher order, pruning is standard. That being said, why do you have different orders of approximation in estimation and stoch_simul?
Thank you for your response, Dr. Pfeifer. I don’t understand what you mean by
Why don’t you use stoch_simul(order=1)?
Because I have many quadratic adjustment costs and based on what I have read in the forum 2nd order approximation should be used to capture their effects better. Also, if I am not wrong, though i may be, similar papers use 2nd order approx. I just figured the 2nd order approx. is the norm for simulations that’s why I use it. Am I in the wrong? Can I also ask what this has to do with the estimation() command? My estimation command doesn’t have any approx. order setting in it.
This is my estimation command:
estimation(plot_priors = 0, datafile = data1, mode_compute = 9, mh_replic = 1000000, mh_nblocks=2, mh_drop=0.25, mh_jscale=0.3, conf_sig = 0.95, mode_check);
The estimation-command by default uses order=1. Thus, it’s rather unusual to have order=2 in simulations (unless you do welfare analysis)
Oh, I am sorry I didnt read this in the manual. So should i use 2nd order in both estimation and simulation or 1st order in both? What is the norm in dsge papers that do not study the welfare effects? Do typical medium scale DSGE model papers like those of Christiano et. al. and Matteo Iacoviello use 1st order or 2nd order approximation (the ones without welfare analysis)?