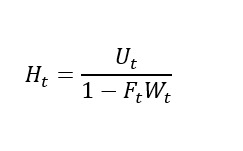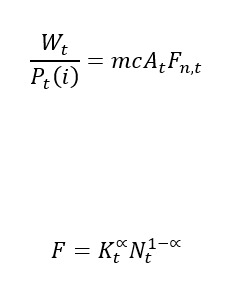Hi,
I have a question regarding log linearisation.
To show my problem I introduce first a easy function.
For Example: Y_t/A_t —> log lin form will be y_head - a_head.
Now I imagine following function, which has no connection to the fct above, I will just try to understand the mathematics in this problem. I do not know how to log linearize the fraction with a sum which is mulitplicative. It will help me a lot if some can solve this equation.
The letters also have no economic meaning.
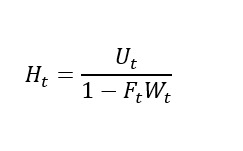
First, do a multivariate first order Taylor approximation:
1\left( {{H_t} - H} \right) = \frac{1}{{1 - FW}}\left( {{U_t} - U} \right) + \left( { - \frac{{{U}}}{{{{\left( {1 - FW} \right)}^2}}}} \right)\left( { - W} \right)\left( {{F_t} - F} \right) + \left( { - \frac{U}{{{{\left( {1 - FW} \right)}^2}}}} \right)\left( { - F} \right)\left( {{W_t} - W} \right)
Then expand the fractions:
H\frac{{\left( {{H_t} - H} \right)}}{H} = \frac{U}{{1 - FW}}\frac{{\left( {{U_t} - U} \right)}}{U} + \left( {\frac{{{U}}}{{{{\left( {1 - FW} \right)}^2}}}} \right)\left( {FW} \right)\frac{{\left( {{F_t} - F} \right)}}{F} + \left( {\frac{U}{{{{\left( {1 - FW} \right)}^2}}}} \right)\left( {FW} \right)\frac{{\left( {{W_t} - W} \right)}}{W}
Then use that in steady state
H = \frac{U}{{1 - FW}}
to get
{{\hat H}_t} = {{\hat U}_t} + \left( {\frac{{FW}}{{1 - FW}}} \right)\left( {{{\hat F}_t} + {{\hat W}_t}} \right)
Please check that I did not do stupid mistakes.
1 Like
Hi Mister Pfeier, that really helped me. Thanks a lot.
I have one more question :).
If I want to linearise one optimility condition:
for example this one
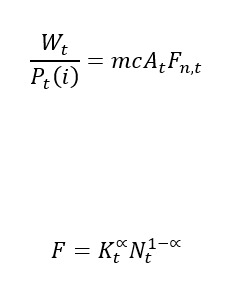
In this case, F is already differentiated in the optimility condition. And the function is known. Of course, the derivation of the Function to N is no problem.
But if i want to take a multivariate Taylor Approx, do I have to differentiate F_n to just N or also K ?
Have a nice Weekend:)
F_n=\left(\frac{K_t}{N_t}\right)^\alpha is clearly a function of labor and capital. You need to take the partial derivative with respect to both.