Intertemporal equation does not hold at t=0 in stochastic simulation

General DSGE Modeling
1

Dear all and Professor Pfeifer,

I have a question about the DSGE modeling and its stochastic simulation results.

I have the following equation:

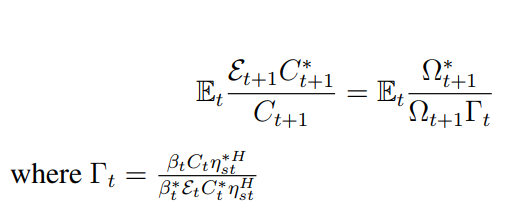
image

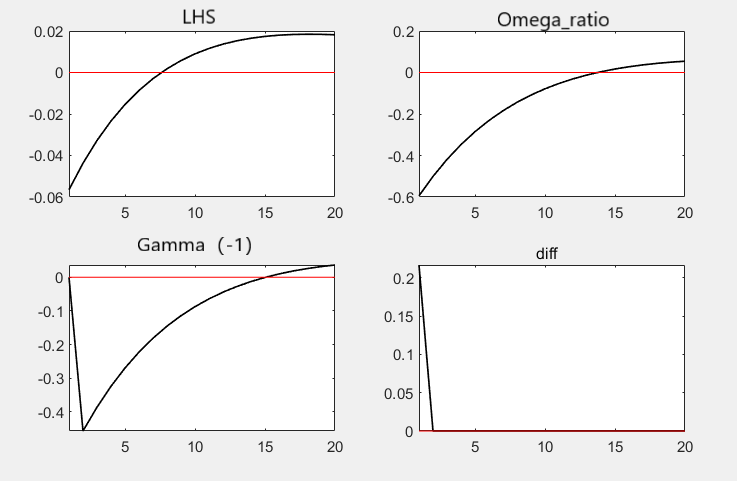
I thought the equation holds and therefore the IRFs of its difference should be zero at all horizons then, but it seems not. At t=0, when the shock hits, the equation does not hold as shown in the figure below:

im2
im2737×481 19.2 KB

In the figure, if we shift all the time scripts one period back, at time t=0, the IRF of the Gamma(-1) term is zero as expected. However, the IRF of diff (the LHS minus the RHS) is not zero at time t=0. The IRFs of diff is zero when t>=1, which means the equation holds only when t>=1. So why it does not hold at time t=0? And at time t=0, since the equation does not hold, how are the LHS and Omega_ratio term determiend then?

I would really appreciate that if anyone could help!

Thanks so much!

Best,
Bob

2

I would need to see the codes.

4

Why would a condition that holds in expectations hold at time t on impact. After all, this condition is supposed to hold on average, but not for a given shock. Starting from t=1, the law of iterated expectations tells you that the condition needs to be satisfied again.

5

Dear Professor Pfeifer,

Thanks for your kind reply! I see. I may really need to look into the model more deeply and see how it works.

Thanks again!

Best,
Bob