Interpretation of Leeper (2009)

General DSGE Modeling Replication Attempts
1

Hi all,

I made a quick and simplified version of Leeper (Dynamics of Fiscal Financing in the US); I have capital tax, labour tax, and government spending. There is no transfers and no consumption tax like in the original Leeper model.

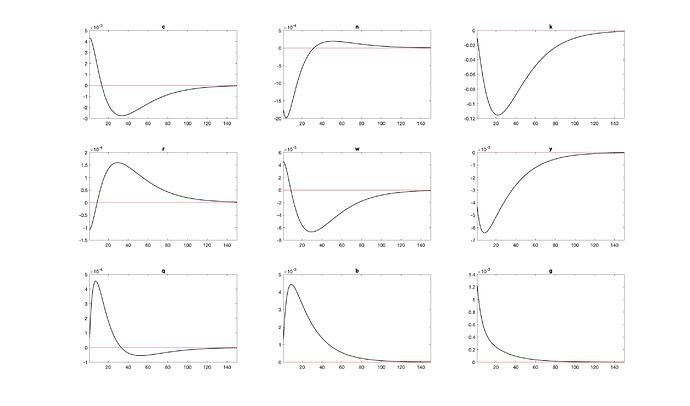
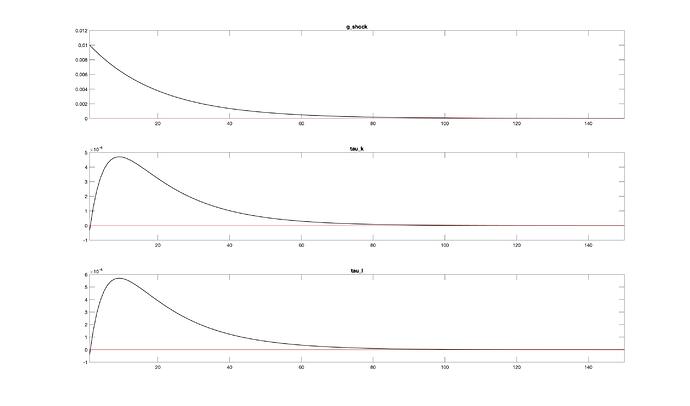
In the IRF plot, it shows that output declined with higher government spending. I am not sure why would this be the case?

The goods market which is y = c + i + g, means that if g increases, then y should increase as well. The only way that increase in g leads to decrease in y, is if investment decrease. Does this mean that household now switch from investing in capital to investing in government bonds?

1
12880×1698 139 KB

2
22880×1698 92.3 KB

Code;

var c n k z r w y q b g g_shock tau_k tau_l;
varexo e_z e_g;
parameters beta theta delta rho a psi psi_g;

beta = 0.99;
delta = 0.025;
theta = 0.36;
a = 1.72;
rho = 0.95;
psi = 0.5;
psi_g = 0.5;

params = [beta theta delta a psi];
init = [0.5 0.1 1 0.1 0.1 0.1 0.01];

options = optimset('Display','iter');
[ss,Fval,exitflag] = fsolve('rbc_gov_ss',init,options,params);

model;
// First order conditions for households.
(((1 - tau_l) * w) / c)  = a / (1 - n);
beta * ((1/c(+1)) * (1 - tau_k) * (r(+1) + 1 - delta)) = (1 / c);
beta * (1/c(+1)) = (q / c);

// Household budget constraints.
c + k + q * b = (1 - tau_l) * w * n + (1 - tau_k) * r * k(-1) + (1 - delta) * k(-1) + b(-1);

// Firm production.
y = exp(z) * k(-1)^(theta) * n^(1 - theta);
w = (1 - theta) * exp(z) * k(-1)^(theta) * n^(-theta);
r = theta * exp(z) * k(-1)^(theta - 1) * n^(1 - theta);

z = rho*(z(-1)) + e_z;

// Government budget constraint.
tau_l * w * n + tau_k * r * k(-1) + q * b = b(-1) + g;

// Government rules
//t / ((1/beta)* (0.3396*1.23358) - (0.0922*1.23358)) = - psi * log(b / (0.3396*1.23358)) - psi_g*log(y/1.23358) + t_shock;
//g / (0.0922*1.23358) = - psi * log(b / (0.3396*1.23358)) - psi_g*log(y/1.23358) + g_shock;
//tau_l / 0.223 = psi * log(b / (0.3396*1.23358)) + psi_g*log(y/1.23358);
//tau_k / 0.184 = psi * log(b / (0.3396*1.23358)) + psi_g*log(y/1.23358);
//t / (0.223 * steady_state(w) * steady_state(n) + 0.184 * steady_state(r) * steady_state(k) + steady_state(q)*steady_state(b)-0.0922*steady_state(y)-steady_state(b))  = - psi * (b / (0.3396*steady_state(y)))  - psi_g * (y/steady_state(y))  + t_shock;
g / (0.0922 * steady_state(y))  = - psi * (b / (0.3396*steady_state(y)))  - psi_g * (y/steady_state(y)) + g_shock;
tau_l / 0.223 = psi * (b / (0.3396*steady_state(y)))  + psi_g * (y/steady_state(y));
tau_k / 0.184 = psi * (b / (0.3396*steady_state(y)))  + psi_g * (y/steady_state(y));

// Gov shocks
//t_shock = rho*(t_shock(-1)) + e_t;
g_shock = rho*(g_shock(-1)) + e_g;

end;

initval;
z = 0;
c = ss(1);
n = ss(2);
k = ss(3);
r = ss(4);
w = ss(5);
y = ss(6);
q = ss(7);
b = 0.3396*1.2815;
g = 0.0922*1.2815;
//t = (1/beta)* b - g;
tau_k = 0.184;
tau_l = 0.223;
end;

model_diagnostics;
resid;
steady;

shocks;
var e_z = 0.01^2;
var e_g = 0.01^2;
//var e_t = 0.01^2;

end;

stoch_simul(periods=2000, drop=200,irf = 150,order=1);
2

Hmmm…which equation in your model captures this relationship (that is, the equilibrium condition)? Seems it is missing in your model.

Goods market should clear in the model, maybe. That is, you need to put the equilibrium condition y = c + i + g in there.

3

I did not specify that equation in the model specifically, because I already specify the labor, capital, and bond markets equations.

If 3 of the market clears, the 4th one will also clear.

4

You can always trace the dynamics in the model. For example, you have

y = exp(z) * k(-1)^(theta) * n^(1 - theta);

So because n falls and k falls y also falls, I think. But why n and k fall in your model?

You can always trace the shock from where it began given your model is correct. e_g goes up, g_shock goes up and g goes up. Then what should the government do to ensure its budget constraint tau_l * w * n + tau_k * r * k(-1) + q * b = b(-1) + g; is satisfied. As g increases, the government chooses q, b, tau_k, and tau_l to fund the higher g. In your model b goes up and q goes up. As q goes up, c goes up because of this equation: beta * (1/c(+1)) = (q / c)…i.e., to ensure equality holds. As c goes up, n falls and w increases to ensure the equality in this equation holds: (((1 - tau_l) * w) / c) = a / (1 - n);. The fall in n outweighs the higher w so capita falls in this equation: w = (1 - theta) * exp(z) * k(-1)^(theta) * n^(-theta);. The total effect of lower k(-1) and lower n on r is that r falls in this equation: r = theta * exp(z) * k(-1)^(theta - 1) * n^(1 - theta);

But why y falls in your model? Because capital falls and labor falls, I think. Why do they fall? You can trace it in the model. A better guide is Gali (2015). How he traces shocks is nice, kind of. He derives each equation as the variable he cares about on the left-hand side, and what explains that variable on the right-hand side, so it is easy to trace the shocks. Not sure about your model but given the equations you have, y falls because n and k fall.

Maybe you can replace
c + k + q * b = (1 - tau_l) * w * n + (1 - tau_k) * r * k(-1) + (1 - delta) * k(-1) + b(-1);
with
y = c+i+g.

If you get similar results, then the two are equivalent.

1 Like
5

Models with distortionary taxation are tricky to interpret. The most likely interpretation is that the increase in G causes capital taxes to increase, discouraging investment.

1 Like
6

Thanks!

That is a great explanation.

7

Thanks! Great explanation.