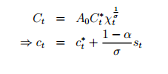How does international risk sharing affects the DSGE model results?

[kofiemma]

In SOE models, there is international risk sharing in the international market. A common form is shown below where consumption depends on the consumption in the rest of the world and the real exchange rate.

However, this equation does not appear in the model’s solution (written in DYNARE). Why is there the need to mention it in the paper as it does not appear to be used in DYNARE?

Let me ask though, what risk is being shared here, intuitively. I know in some macro models (not DSGE), households share risk so that individual consumption varies only with aggregate income (not idiosyncratic income), helping to mitigate the effect of wide volatilities in one’s income on his/her consumption. So in the equations above, I guess if consumption varies with c^*_t and s_t, the household is mitigating some kind of risk. But intuitively I cannot see what risk it is.

[jpfeifer]

1. Which equation is not put into the models?
2. You are sharing risks across countries. The logic is the same as between individuals. Here, countries are subject to country-specific shocks. Part of the risk can be diversified by a risk-sharing arrangement that equalizes marginal utilities across countries.

[kofiemma]

Oh, I see. Many thanks!! I could not see c^*_t in DYNARE (for the paper I read), so I thought c_t = c^*_t + \frac{1-\alpha}{\sigma} s_t was not used. But I see my mistake, i.e., the global goods market clears (C^*_t =Y^*_t), and international risk sharing is being captured through the goods market-clearing condition: Y_t(i) = C^h_t(i) + X_t(i), where X_t = v(\frac{P^h_t}{S_t P^*_t})^{-\eta}C^*_t.

Wanted a hint though how international risk sharing assumption affects the DSGE model results because I see some SOE models with no international risk sharing like this one (NTG.pdf (243.8 KB)).

My current model has no international risk sharing, If I assume there is international risk sharing, I guess I can do something like this?
NX_t = X_t - Imports = v(\frac{P^h_t}{S_t P^*_t})^{-\eta}C^*_t - Imports
And then I can replace C^*_t using the risk sharing condition:

I am not writing the NX equation in full though. But hopefully, it isn’t confusing. Thanks!!

[HelloDynare]

Sorry for bothering your discussion. I remember the international risk sharing condition is associated with the complete international financial market assumption (Arrow securities), while in your attachment, the budget constraint is an incomplete type.

[kofiemma]

Oh nice! Many thanks! I think my model is ok then (i.e., without international risk sharing) since the foreign asset in the household’s budget constraint (in my model) is not Arrow securities.

May I ask though, how does it affect the DSGE model results whether or not assets are assumed to be Arrow securities? Maybe arrow securities are more realistic, but any other known benefits regarding the simulation of the model?

[jpfeifer]

@HelloDynare Risk sharing can be complete or partial. Full risk sharing indeed involves Arrow or Arrow-Debreu securities. It implies that marginal utilities are equalized across all states of the world.
Incomplete risk sharing via non-contingent securities only allows for limited risk-sharing. There will be some equalization of marginal utilities but it will be incomplete, i.e. not be state by state, but rather on average (the Euler equation features an expectation on the right)
@kofiemma Complete international financial markets are definitely unrealistic. Incomplete markets usually perform better. See e.g.

International Risk Sharing and the Transmission of Productivity Shocks

[RodrigoTM]

Professor Pfeifer, may I ask you some related question?
I understood that when I have arrow securities, the risk-sharing is complete so it will be true state by state. This occurs in Gali’s book in open economy chapter.

What I did not understand is that if I write the lagrangian of the Gali’s problem:

L=\sum\beta^t E_0 \bigg\{ U(C_t,N_t) + \lambda_t \big[ D_t+W_t N_t + T_t -P_t C_t -Q_{t,t+1} D_{t+1} \big]\bigg\}

It seems to me that the derivative wrt D_{t+1} should be:

\lambda_t Q_{t,t+1} = \beta E_t \{ \lambda_{t+1} \}

Using the other FOC:

U_c(C_t)= \lambda_t P_t \Rightarrow \frac{U_c(C_{t+1})}{U_c(C_t)}\frac{P_t}{P_{t+1}}=\frac{\lambda_{t+1}}{\lambda_t}

We will have:

E_t \bigg\{ \beta \frac{U_c(C_{t+1})}{U_c(C_t)}\frac{P_t}{P_{t+1}} \bigg\} =Q_{t,t+1}

Then the risk-sharing condition (using a similar Lagrangian for the foreign economy) would be:

E_t \bigg\{ \beta \frac{U_c(C_{t+1})}{U_c(C_t)}\frac{P_t}{P_{t+1}} \bigg\} = E_t \bigg\{ \beta \frac{U_c(C^*_{t+1})}{U_c(C^*_t)}\frac{P^*_t}{P^*_{t+1}} \frac{E_{t}}{E_{t+1}} \bigg\}

So it only occurs on average. I think I am wrong in some place but I cannot see where is the mistake. Would you help me, please?

[jpfeifer]

Your setup above does not feature a full set of securities, but only one security. The expected value already implies that this is not contingent on states.

[RodrigoTM]

Thanks for your answer, professor Pfeifer.
I think I did not express myself correctly. What I want to know it is why in Gali’s book setup (in open economy), the risk-sharing condition occurs not only in average. I think that setup feature a full set of securities.
The risk-sharing in Gali’s is:

c_t=c_t^* + \frac{1}{\sigma} q_t (Eq 1)

The budget constraint is:

P_t C_t +E_t\{Q_{t,t+1} D_{t+1}\} \leq D_t +W_t N_t +T_t

He says that Q_{t,t+1} is the stochastic discount factor and

Q_{t,t+1} \equiv \frac{V_{t,t+1}}{\xi_{t,t+1}}

where V_{t,t+1} is the period t price of and Arrow security if a specific state of nature is realized in t+1

Henceforth is my interpretation of Gali’s. I would like to know if I understood everything correctly.
If the previous equation if verified for every state of nature i, there is a full set of arrow securities.
Hence D_{t+1} may be interpreted a vector of the quantities of each arrow security is bought in t. Each row of this vector is D_{t+1}^i.
I am assuming finite states (I do not know how it would be with infinite states).

In this case, one can write:

Q_{t,t+1} \equiv \frac{V_{t,t+1}^{j,i}}{\xi_{t,t+1}^{j,i}}

where:
\xi_{t,t+1}^{j,i} is the probability to pass from state j in t to state i in t+1

V_{t,t+1}^{j,i} is the price of a arrow security that pays one unit of domestic currency if state i is realized in t+1 given that the state in t is j.

The bugdget constraint could be rewritten in:

P_t C_t + \sum_{i \in I} V_{t,t+1}^{j,i} D_{t+1}^i \leq D_t^k + W_t N_t +T_t

where D_t^k is the quantity bought for state k (the state realized in t).

If I am right until here, it means that the Lagrangian is:

L=\sum \beta^t E_0 \bigg\{ U(C_t,N_t) +\lambda_t \big[ D_t^k + W_t N_t +T_t -P_t C_t - \sum_{i \in I} V_{t,t+1}^{j,i} D_{t+1}^i \big] \bigg\}

where I comprises all the possible states.

Then the FOC wrt D_{t+1}^i is (not so sure about the first equation):

\lambda_t V_{t,t+1}^{j,i}=\beta E_t \{ \lambda_{t+1} \} \Rightarrow \lambda_t V_{t,t+1}^{j,i}=\beta \lambda_{t+1} \xi_{t,t+1}^{j,i} \Rightarrow \frac{\lambda_{t+1}}{\lambda_t} = \frac{1}{\beta}\frac{V_{t,t+1}^{j,i}}{\xi_{t,t+1}^{j,i}} (Eq 2)

If it is right that (Eq 2) holds for every states (j,i) , then

\frac{\lambda_{t+1}}{\lambda_t} = \frac{1}{\beta}Q_{t,t+1}

And then I can see that risk-sharing condition happens not only in average as in (Eq 1)

Is there any problem with my understanding?
Thank you again.

[jpfeifer]

Yes, the important part is the timing of the risk sharing equation. It does not involve expectations, but is contemporaneous. As such, it will hold for any realization of the states.