Helpful Dynare experts,
I am trying to replicate Andolfatto (1996) (Business Cycles and Labor-Market Search on JSTOR). My .mod file seems to be working. (The only difference between the original model and the m.mod is the exogenous shock, which was not normally distributed in the original paper.) However, the results of my simulations do not look like the original paper. This is clear just from the standard deviations; the standard deviation of L (hours per worker) divided by the standard deviation of y (output) is much too low, and the similarly-defined relative standard deviation of c (consumption) is much too high.
I do not know where my mistake could be. Since the model runs well, I doubt this is a typo problem. It seems more likely that I am fundamentally misunderstanding something about the original paper and how it relates to what I am doing in Dynare.
Thank you in advance for any insight you can give. Below you will find a picture of the results I am trying to replicate, a picture of the results I am getting, my .mod file, and the in-paper description of the numerical simulation used.
Matt
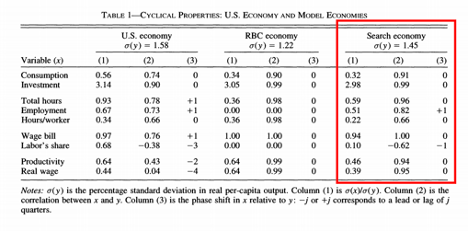
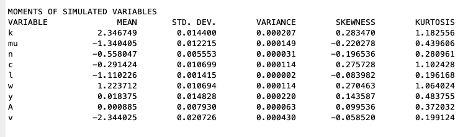
andolfatto_v8.mod (2.9 KB)
With the parameter values so determined, the equilibrium may now be computed numerically. The computation procedure uses an algorithm suggested by Wilbur Coleman II (1990). Essentially, the procedure is to find function evaluations that satisfy the system (P1)- (P6) at discrete points on a state space. The true solution functions are then approximated by piecewise linear interpolations of these function evaluations… A corresponding set of statistics, generated by the different model economies, was constructed by using the equilibrium decision rules to simulate time-series 5000 periods in length. (p. 121-122)